Rozwiązanie
Krok 1. Przeniesienie wyrazów na lewą stronę.
Zanim zaczniemy cokolwiek obliczać, musimy przenieść wszystkie liczby na lewą stronę, tak aby po prawej stronie mieć jedynie zero. W związku z tym:
$$3x^2-2x-9\ge7 \\
3x^2-2x-16\ge0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Chcąc rozwiązać nierówność musimy sprawdzić jakie mamy miejsca zerowe, czyli musimy sprawdzić dla jakich argumentów \(3x^2-2x-16=0\). Musimy więc rozwiązać równanie kwadratowe w postaci ogólnej, a to oznacza, że z pomocą przyjdzie nam więc niezawodna delta.
Współczynniki: \(a=3,\;b=-2,\;c=-16\)
$$Δ=b^2-4ac=(-2)^2-4\cdot3\cdot(-16)=4-(-192)=4+192=196 \\
\sqrt{Δ}=\sqrt{196}=14$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-2)-14}{2\cdot3}=\frac{2-14}{6}=\frac{-12}{6}=-2 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-2)+14}{2\cdot3}=\frac{2+14}{6}=\frac{16}{6}=\frac{8}{3}$$
Krok 3. Szkicowanie wykresu paraboli.
Zaznaczamy na osi obliczone miejsca zerowe i rysujemy przechodzącą przez te punkty parabolę z ramionami skierowanymi do góry (bo współczynnik \(a\) jest dodatni).
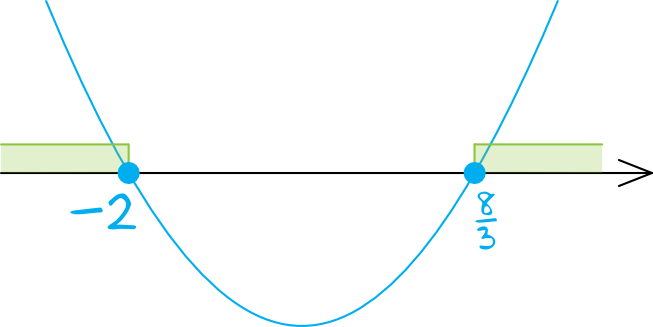
Krok 4. Odczytanie rozwiązania.
Szukamy argumentów, dla których nierówność przyjmuje wartości większe od zera lub równe zero, czyli patrzymy się na to, co znalazło się nad osią lub na osi. W związku z tym rozwiązaniem tej nierówności jest suma przedziałów:
$$x\in(-\infty;-2\rangle\cup\langle\frac{8}{3};+\infty)$$