Rozwiązanie
Krok 1. Doprowadzenie nierówności do postaci ogólnej.
Spróbujmy doprowadzić całość do dobrze znanej nam postaci ogólnej, dzięki czemu będziemy mogli za chwilę skorzystać z delty. Wymnażając więc to co jest po lewej stronie i przenosząc wszystkie wyrazy z prawej na lewą stronę, otrzymamy:
$$3x(x+1)\gt x^2+x+24 \\
3x^2+3x\gt x^2+x+24 \\
2x^2+2x-24\gt0$$
Możemy jeszcze (choć nie musimy) podzielić wszystko przez \(2\), dzięki czemu będziemy bazować na mniejszych liczbach. Otrzymamy wtedy nierówność:
$$x^2+x-12\gt0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=1,\;b=1,\;c=-12\)
$$Δ=b^2-4ac=1^2-4\cdot1\cdot(-12)=1-(-48)=1+48=49 \\
\sqrt{Δ}=\sqrt{49}=7$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-1-7}{2\cdot1}=\frac{-8}{2}=-4 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-1+7}{2\cdot1}=\frac{6}{2}=3$$
Krok 3. Szkicowanie wykresu paraboli.
Współczynnik kierunkowy \(a\) jest dodatni (bo \(a=1\), więc parabola będzie mieć ramiona skierowane do góry. Zaznaczamy więc na osi wyznaczone miejsca zerowe \(x=-4\) oraz \(x=3\) (kropki będą niezamalowane, bo w nierówności wystąpił znak \(\gt\)) i rysujemy parabolę:
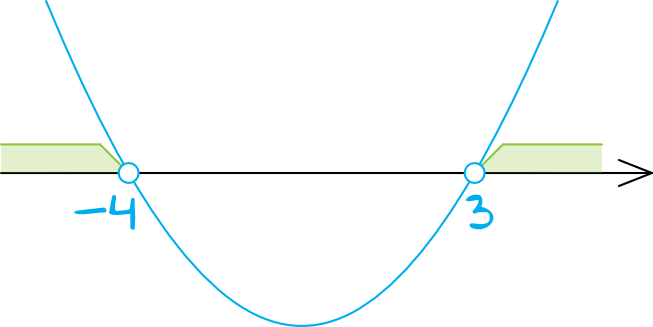
Krok 4. Odczytanie rozwiązania.
Interesują nas wartości większe od zera, zatem interesuje nas to co znalazło się nad osią. To oznacza, że rozwiązaniem tej nierówności jest suma przedziałów:
$$x\in(-\infty;-4)\cup(3;+\infty)$$