Rozwiązanie
Krok 1. Doprowadzenie nierówności do postaci ogólnej.
Zanim zaczniemy liczyć deltę, to musimy przenieść wszystkie wyrazy na lewą stronę, doprowadzając nierówność do postaci ogólnej, zatem:
$$(2x-5)(3-x) \gt -66 \\
6x-2x^2-15+5x \gt -66 \\
6x-2x^2-15+5x+66 \gt 0 \\
-2x^2+11x+51\gt0$$
Krok 2. Wyznaczenie miejsc zerowych.
Teraz zgodnie z zasadami rozwiązywania nierówności szukamy miejsc zerowych, czyli przyrównujemy wartość \(-2x^2+11x+51\) do zera. Mamy więc do rozwiązania równanie kwadratowe w postaci ogólnej \(-2x^2+11x+51=0\), które rozwiążemy klasycznie obliczając deltę:
Współczynniki: \(a=-2,\;b=11,\;c=51\)
$$Δ=b^2-4ac=11^2-4\cdot(-2)\cdot51=121-(-408)=121+408=529 \\
\sqrt{Δ}=\sqrt{529}=23$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-11-23}{2\cdot(-2)}=\frac{-34}{-4}=8\frac{1}{2} \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-11+23}{2\cdot(-2)}=\frac{12}{-4}=-3$$
Krok 3. Szkicowanie wykresu paraboli.
Parabola będzie mieć ramiona skierowane do dołu, bo współczynnik kierunkowy \(a\) jest ujemny. Rysujemy oś, zaznaczamy wyznaczone miejsce zerowe i szkicujemy parabolę:
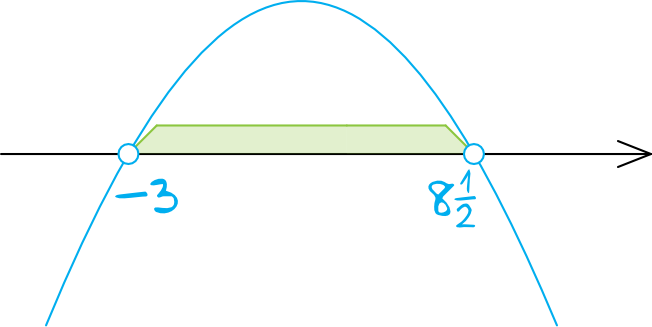
Krok 4. Odczytanie rozwiązania.
Interesują nas wartości większe od zera, zatem patrzymy się na to co jest nad osią. To oznacza, że rozwiązaniem nierówności jest przedział.
$$x\in\left(-3;8\frac{1}{2}\right)$$