Rozwiązanie
To zadanie moglibyśmy rozwiązać jak klasyczną nierówność (czyli np. metodą delty), pamiętając o tym by najpierw przenieść wszystkie wyrazy na lewą stronę. Jednak w tym zadaniu proszą nas o graficzne rozwiązanie podanej nierówności, zatem powinniśmy zgodnie z poleceniem pokusić się o rozwiązanie tej nierówności rysując po prostu wykresy funkcji, których wzory znalazły się po lewej i prawej stronie nierówności, czyli \(x^2\) oraz \(x+2\).
Krok 1. Sporządzenie wykresów funkcji \(x^2\) oraz \(x+2\).
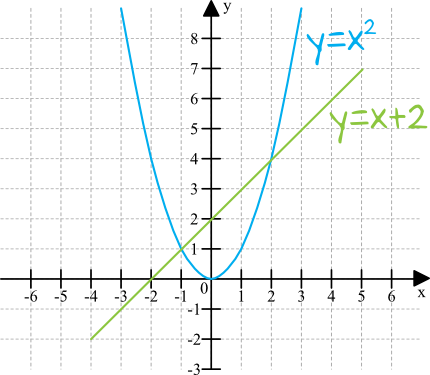
Z racji tego, iż mamy rozwiązać graficznie naszą nierówność, to nasz rysunek powinien być jak najdokładniejszy. W szczególności musimy zwrócić uwagę na to, by parabola \(x^2\) miała wierzchołek w początku układu współrzędnych, a prosta \(x+2\) przecinała oś igreków w punkcie \((0;2)\).
Krok 2. Interpretacja rysunku i odczytanie rozwiązań nierówności.
Po dokładnym narysowaniu obydwu wykresów widzimy że przecięły się one w dwóch punktach: \(A=(-1;-1)\) oraz \(B=(2;4)\). To właśnie te punkty będą kluczowymi do wyznaczenia rozwiązań nierówności. Interesuje nas sytuacja w której wyrażenie po lewej stronie jest większe od tego po prawej stronie, czyli interesują nas wszystkie te miejsca w których po prostu parabola \(x^2\) jest wyżej (czyli przyjmuje większe wartości) od prostej \(x+2\). Rozwiązaniem tej nierówności będzie więc:
$$x\in(-\infty;-1)\cup(2;+\infty)$$