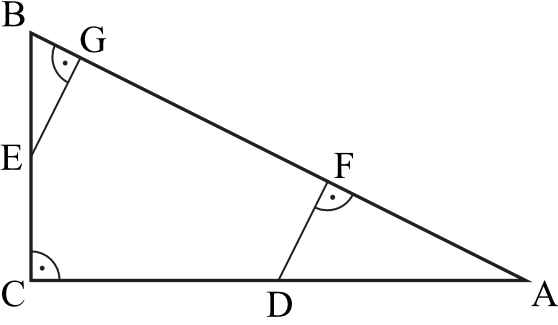
Punkty \(D\) i \(E\) są środkami przyprostokątnych \(AC\) i \(BC\) trójkąta prostokątnego \(ABC\). Punkty \(F\) i \(G\) leżą na przeciwprostokątnej \(AB\) tak, że odcinki \(DF\) i \(EG\) są do niej prostopadłe (zobacz rysunek). Pole trójkąta \(BGE\) jest równe \(1\), a pole trójkąta \(AFD\) jest równe \(4\).
Zatem pole trójkąta \(ABC\) jest równe:
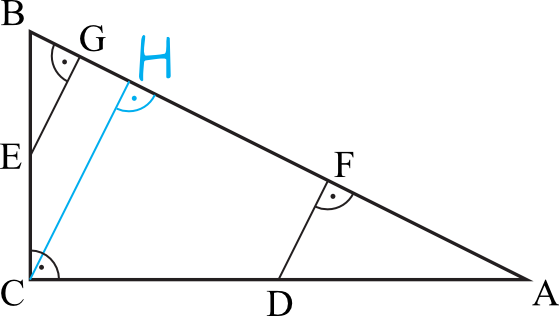
Dorysowalismy sobie wysokość \(CH\) trójkąta \(ABC\). Podzieliła nam ona trójkąt na dwa mniejsze trójkąty – \(ACH\) oraz \(BCH\). Suma pól powierzchni tych trójkątów da nam poszukiwane pole trójkąta \(ABC\).
Skorzystamy tutaj ze skali podobieństwa trójkątów \(ACH\) oraz \(AFD\). Z treści zadania wynika, że \(k=\frac{|AC|}{|AD|}=2\). Z geometrii wiemy, że stosunek dwóch pól figur podobnych jest równy \(k^2\), czyli w naszym przypadku \(k^2=2^2=4\). Skoro pole trójkąta \(AFD\) jest równe \(4\), a pole \(ACH\) musi być czterokrotnie większe, to \(P_{ACH}=4\cdot4=16\).
Analogicznie możemy przeanalizować parę trójkątów \(BCH\) oraz \(BGE\). Skoro \(k=\frac{|BH|}{|BG|}=2\), to ponownie pole trójkąta \(BCH\) będzie czterokrotnie większe od pola trójkąta \(BGE\). Pole trójkąta \(BCH\) jest więc równe \(P_{BCH}=4\cdot1=4\).
$$P_{ABC}=P_{ACH}+P_{BCH} \\
P_{ABC}=16+4 \\
P_{ABC}=20$$
D. \(20\)


skąd wzięło się tam 2?
Chodzi o k=2?
Z treści zadania wynika, że odcinek AC jest dwa razy dłuższy od AD (bo punkt D jest dokładnie środkiem odcinka AC), stąd też k=2 :)
Ewentualnie moglibyśmy zapisać, że |AC|=x oraz |AD|=1/2x i wtedy k=x przez 1/2x, co daje nam właśnie 2 :)
Dlaczego nie można od razu zastosować skali podobieństwa w trójkącie ABC i w trójkącie DAF? Skoro one są do siebie podobne z cechy KKK? Trzeba koniecznie poprowadzić tę wysokość H?
A jaka jest skala podobieństwa trójkątów ABC i DAF? :)