Punkty A oraz B leżą na okręgu o środku O. Proste k i l są styczne do tego okręgu w punktach

Punkty $A$ oraz $B$ leżą na okręgu o środku $O$. Proste $k$ i $l$ są styczne do tego okręgu w punktach – odpowiednio – $A$ i $B$. Te proste przecinają się w punkcie $S$ i tworzą kąt o mierze $76°$ (zobacz rysunek).

Miara kąta $OBA$ jest równa:

A. $52°$

B. $26°$

C. $14°$

D. $38°$

Rozwiązanie

Z własności stycznych do okręgu wynika, że odcinki $AS$ oraz $BS$ mają jednakową miarę. Skoro tak, to trójkąt $ASB$ jest równoramienny, czyli kąty przy podstawie $AB$ będą mieć jednakową miarę. Skoro więc kąt $ASB$ ma miarę $76°$, to na dwa pozostałe trójkąty zostaje nam $180°-76°=104°$. To oznacza, że kąty $BAS oraz \(ABS$ będą mieć miarę równą:
$$104°:2=52°$$

Drugą kluczową własności stycznych do okręgu jest fakt, iż styczna tworzy z promieniem okręgu kąt prosty. Skoro tak, to otrzymamy taką oto sytuację:
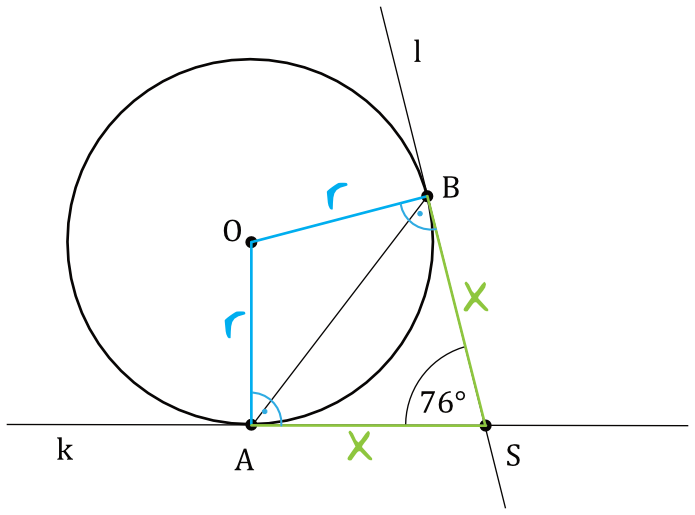
matura z matematyki

W związku z tym miara kąta $OBA$ jest równa:
$$|\sphericalangle OBA|=90°-52°=38°$$

Odpowiedź

Zadania

Punkty A oraz B leżą na okręgu o środku O. Proste k i l są styczne do tego okręgu w punktach

Punkty \(A\) oraz \(B\) leżą na okręgu o środku \(O\). Proste \(k\) i \(l\) są styczne do tego okręgu w punktach – odpowiednio – \(A\) i \(B\). Te proste przecinają się w punkcie \(S\) i tworzą kąt o mierze \(76°\) (zobacz rysunek).

Miara kąta \(OBA\) jest równa:

Punkty \(A\) oraz \(B\) leżą na okręgu o środku \(O\). Proste \(k\) i \(l\) są styczne do tego okręgu w punktach – odpowiednio – \(A\) i \(B\). Te proste przecinają się w punkcie \(S\) i tworzą kąt o mierze \(76°\) (zobacz rysunek). Miara kąta \(OBA\) jest równa:

Punkty \(A\) oraz \(B\) leżą na okręgu o środku \(O\). Proste \(k\) i \(l\) są styczne do tego okręgu w punktach – odpowiednio – \(A\) i \(B\). Te proste przecinają się w punkcie \(S\) i tworzą kąt o mierze \(76°\) (zobacz rysunek).

Miara kąta \(OBA\) jest równa: