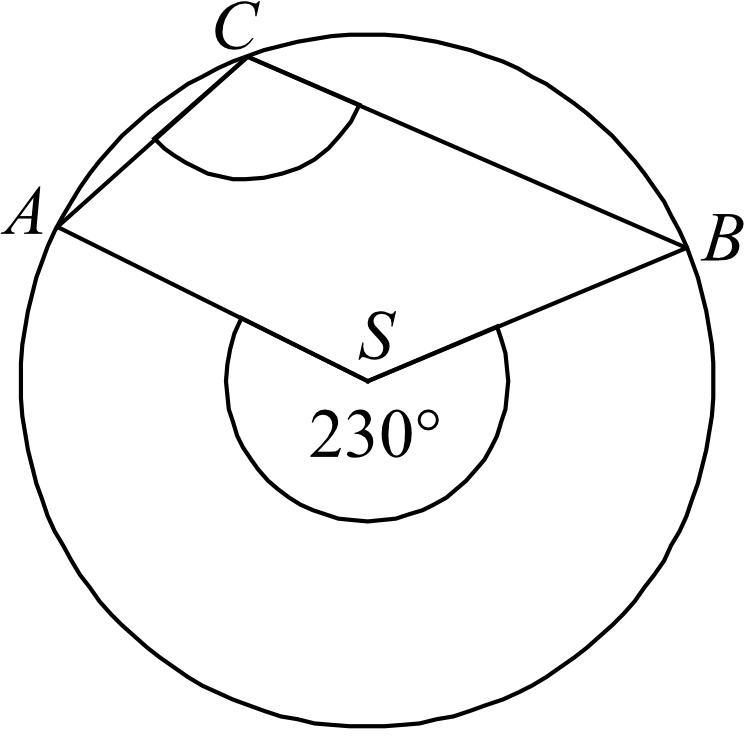
Punkty \(A\), \(B\) i \(C\) leżą na okręgu o środku \(S\) (zobacz rysunek). Miara zaznaczonego kąta wpisanego \(ACB\) jest równa:
\(65°\)
\(100°\)
\(115°\)
\(130°\)
Rozwiązanie:
Korzystamy z zależności między kątem środkowym i kątem wpisanym w okrąg, które są oparte na tym samym łuku (patrz rysunek). Zgodnie z tą zależnością miara kąta środkowego jest dwa razy większa od miary kąta wpisanego. To oznacza, że:
$$|\sphericalangle ACB|=\frac{1}{2}\cdot|\sphericalangle ASB| \\
|\sphericalangle ACB|=\frac{1}{2}\cdot230° \\
|\sphericalangle ACB|=115°$$

Odpowiedź:
C. \(115°\)

