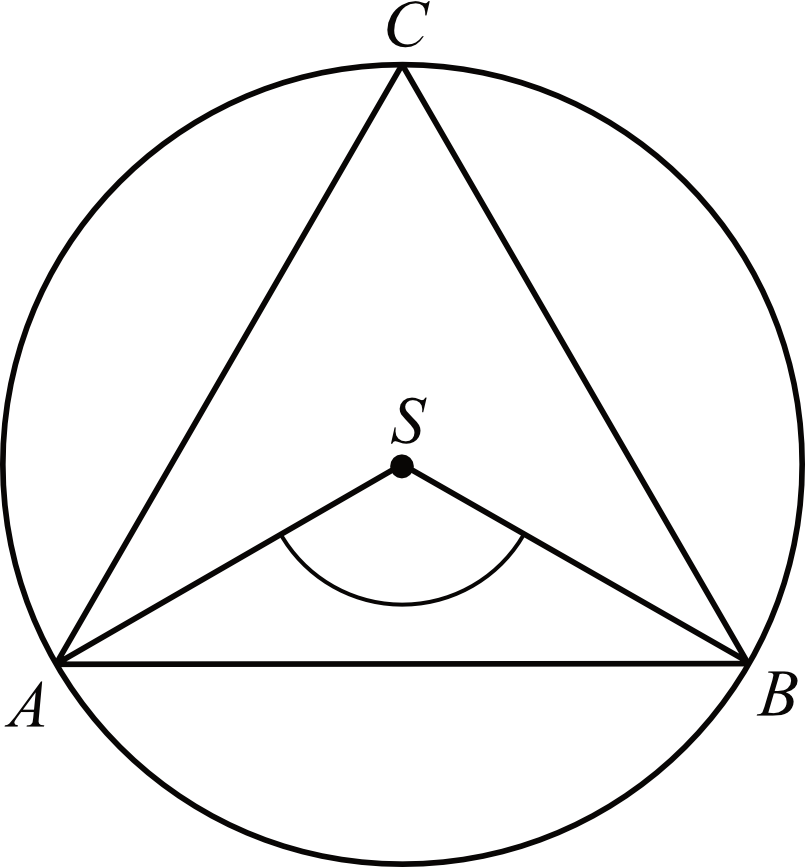
Punkty \(A,B,C\) leżące na okręgu o środku \(S\) są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego \(ASB\) jest równa:
\(120°\)
\(90°\)
\(60°\)
\(30°\)
Rozwiązanie:
Chcąc obliczyć to zadanie wystarczy skorzystać z własności kątów środkowych i wpisanych, pamiętając o tym, że każdy kąt w trójkącie równobocznym ma miarę \(60°\). Widzimy, że kąty \(ACB\) oraz \(ASB\) są oparte na tym samym łuku. Skoro kąt \(ACB\) wpisany na okręgu ma \(60°\), to kąt środkowy \(ASB\) ma \(2\cdot60°\), czyli \(120°\).
Tak na marginesie – to zadanie dałoby się praktycznie rozwiązać bez obliczeń, bo już z samego rysunku widać, że zaznaczony kąt jest kątem rozwartym, a tylko \(120°\) jest takim kątem.
Odpowiedź:
A. \(120°\)

