Rozwiązanie
Krok 1. Wyznaczenie miary kąta \(BAC\).
Powinniśmy dostrzec, że kąt środkowy \(BSC\) o mierze \(\alpha\) jest oparty na tym samym łuku co kąt wpisany \(BAC\). Skoro tak, to miara kąta \(BAC\) będzie połową kąta środkowego, czyli \(|\sphericalangle BAC|=\frac{\alpha}{2}\).
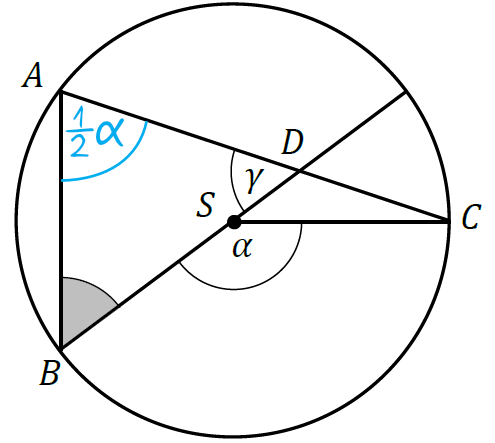
Krok 2. Wyznaczenie miary kąta \(ABD\).
Spójrzmy na trójkąt \(BDA\). Znamy już dwie miary kątów w tym trójkącie, a trzeci jest tym przez nas poszukiwanym. Skoro więc suma kątów w trójkącie jest równa \(180°\), to:
$$|\sphericalangle ABD|=180°-\frac{\alpha}{2}-\gamma$$