Punkty A, B, C i D leżą na okręgu o środku w punkcie O. Cięciwy DB i AC przecinają się w punkcie E

Punkty $A$, $B$, $C$ i $D$ leżą na okręgu o środku w punkcie $O$. Cięciwy $DB$ i $AC$ przecinają się w punkcie $E$, $|\sphericalangle ACB|=55°$ oraz $|\sphericalangle AEB|=140°$ (zobacz rysunek).

Miara kąta $DAC$ jest równa:

A. $45°$

B. $55°$

C. $70°$

D. $85°$

Rozwiązanie

Krok 1. Obliczenie miary kąta $CEB$.
Kąt $CEB$ jest kątem przyległym do znanego nam kąta $AEB$ o mierze $140°$. Suma kątów przyległych jest zawsze równa $180°$, zatem:
$$|\sphericalangle CEB|=180°-140°=40°$$

Krok 2. Obliczenie miary kąta $EBC$.
Spójrzmy na trójkąt $EBC$. Znamy miary dwóch kątów w tym trójkącie, zatem miara trzeciego kąta, czyli kąta $EBC$, będzie równa:
$$|\sphericalangle EBC|=180°-40°-55°=85°$$

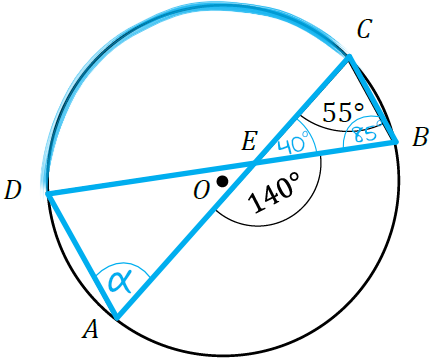
matura z matematyki

Krok 3. Obliczenie miary kąta $DAC$.
Powinniśmy dostrzec, że kąty $EBC$ oraz $DAC$ są kątami wpisanymi, które są oparte na tym samym łuku (na łuku $DC$). Skoro tak, to ich miara musi być jednakowa, zatem:
$$|\sphericalangle DAC|=|\sphericalangle EBC|=85°$$

Odpowiedź

Zadania

Punkty A, B, C i D leżą na okręgu o środku w punkcie O. Cięciwy DB i AC przecinają się w punkcie E

Punkty \(A\), \(B\), \(C\) i \(D\) leżą na okręgu o środku w punkcie \(O\). Cięciwy \(DB\) i \(AC\) przecinają się w punkcie \(E\), \(|\sphericalangle ACB|=55°\) oraz \(|\sphericalangle AEB|=140°\) (zobacz rysunek).

Miara kąta \(DAC\) jest równa:

Punkty \(A\), \(B\), \(C\) i \(D\) leżą na okręgu o środku w punkcie \(O\). Cięciwy \(DB\) i \(AC\) przecinają się w punkcie \(E\), \(|\sphericalangle ACB|=55°\) oraz \(|\sphericalangle AEB|=140°\) (zobacz rysunek). Miara kąta \(DAC\) jest równa:

Punkty \(A\), \(B\), \(C\) i \(D\) leżą na okręgu o środku w punkcie \(O\). Cięciwy \(DB\) i \(AC\) przecinają się w punkcie \(E\), \(|\sphericalangle ACB|=55°\) oraz \(|\sphericalangle AEB|=140°\) (zobacz rysunek).

Miara kąta \(DAC\) jest równa: