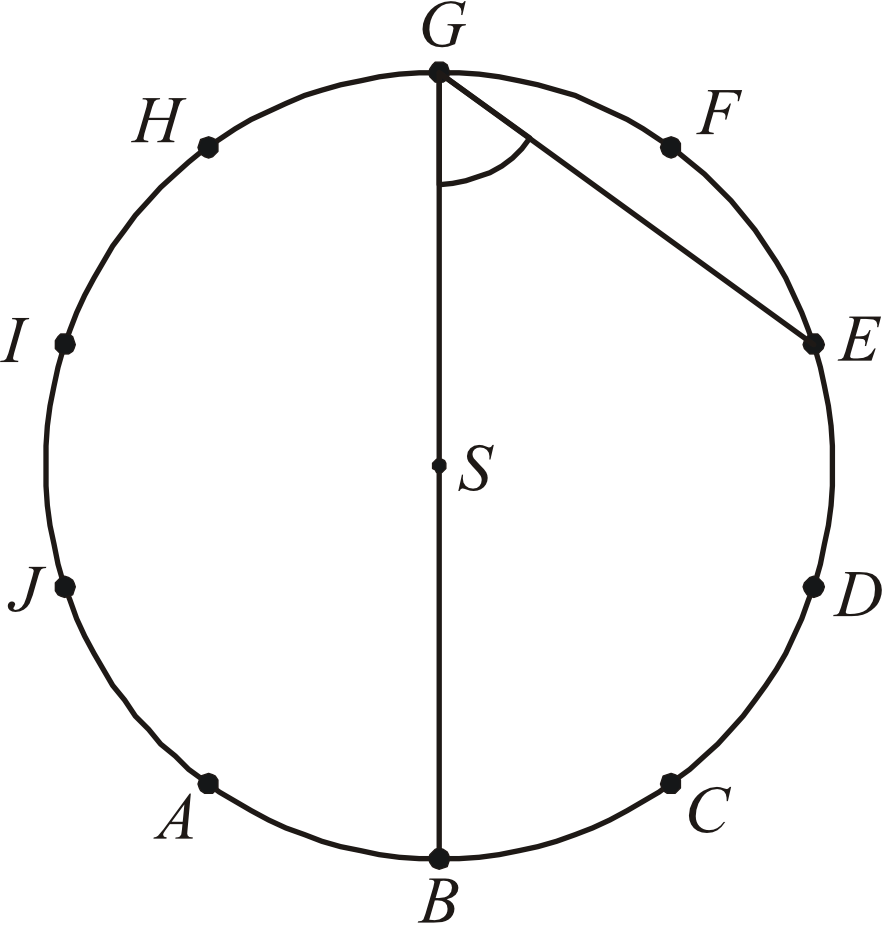
Punkty \(A, B, C, D, E, F, G, H, I, J\) dzielą okrąg o środku \(S\) na \(10\) równych łuków. Oblicz miarę kąta wpisanego \(BGE\) zaznaczonego na rysunku.
\(54°\)
\(72°\)
\(60°\)
\(45°\)
Rozwiązanie:
Krok 1. Obliczenie miary kąta \(BSE\).
Dorysujmy sobie odcinek \(SE\) i obliczmy miarę kąta środkowego \(BSE\).
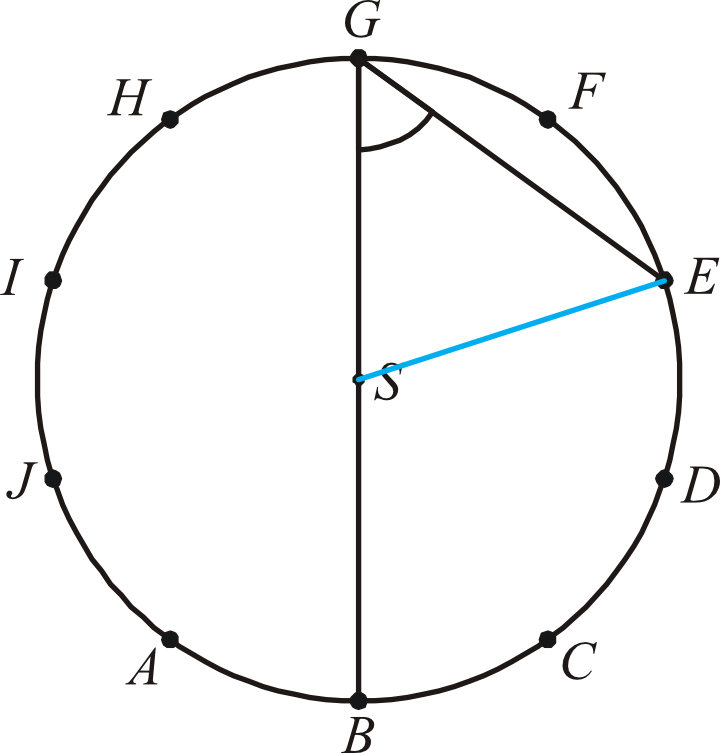
Widzimy, że kąt ten stanowi trzy z dziesięciu „cząstek” kąta pełnego, zatem jego miara jest równa:
$$|\sphericalangle BSE|=\frac{3}{10}\cdot360° \\
|\sphericalangle BSE|=108°$$
Krok 2. Obliczenie miary kąta \(BGE\).
Kąt \(BGE\) jest oparty na tym samym łuku co kąt środkowy \(BSE\), którego miarę obliczyliśmy przed chwilą. W związku z tym zgodnie z własnościami kątów wpisanych i środkowych kąt ten będzie dwa razy mniejszy od kąta \(BSE\):
$$|\sphericalangle BGE|=108°:2 \\
|\sphericalangle BGE|=54°$$
Odpowiedź:
A. \(54°\)

