Punkty \(A, B, C, D\) dzielą okrąg na \(4\) równe łuki. Miara zaznaczonego na rysunku kąta wpisanego \(ACD\) jest równa:

\(90°\)
\(60°\)
\(45°\)
\(30°\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
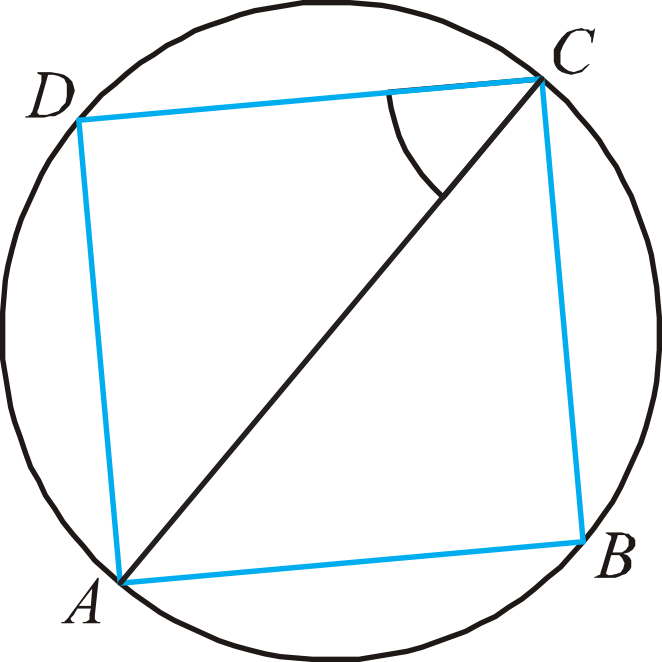
Dzięki informacji, która mówi o tym że punkty \(A, B, C, D\) podzieliły nam okrąg na cztery równe łuki, jesteśmy w stanie stwierdzić, że odległości pomiędzy sąsiednimi punktami na okręgu są identycznej długości, a zaznaczony odcinek \(AC\) jest średnicą tego okręgu. To oznacza, że trójkąt \(ADC\) jest równoramienny i w dodatku prostokątny, bo trójkąt oparty na średnicy jest zawsze prostokątny.
Krok 2. Obliczenie miary kąta \(ACD\).
Jeżeli suma katów w trójkącie prostokątnym \(ACD\) jest równa \(180°\), a kąt \(|\sphericalangle ADC|=90°\), to:
$$|\sphericalangle ACD|+|\sphericalangle DAC|=180°-90°=90°$$
Skoro trójkąt \(ACD\) jest dodatkowo równoramienny to kąty przy podstawie \(AC\) muszą mieć równą miarę. Zatem:
$$|\sphericalangle ACD|=90°:2=45°$$
Odpowiedź:
C. \(45°\)

