Punkty \(A=(-6-2\sqrt{2}, 4-2\sqrt{2})\), \(B=(2+4\sqrt{2}, -6\sqrt{2})\), \(C=(2+6\sqrt{2}, 6-2\sqrt{2})\) są kolejnymi wierzchołkami równoległoboku \(ABCD\). Przekątne tego równoległoboku przecinają się w punkcie:
Spróbujmy mniej więcej zaznaczyć w układzie współrzędnych punkty \(A\), \(B\) oraz \(C\):
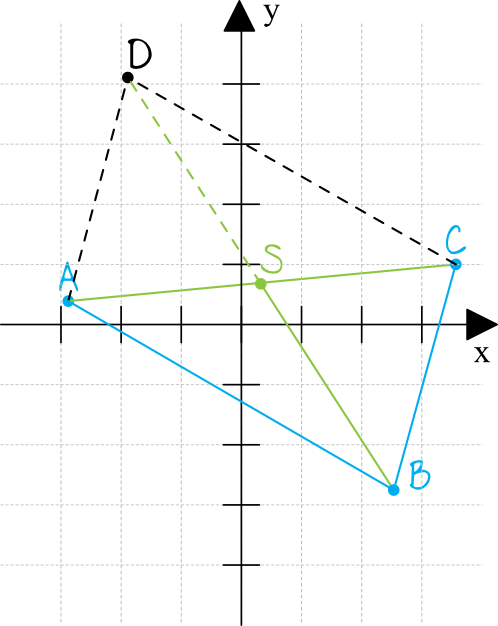
Nie znamy współrzędnych punktu \(D\) (na rysunku jest on tylko by zobrazować sobie jak wygląda ten równoległobok), ale nie jest nam on na szczęście potrzebny. Przekątne równoległoboku przecinają się w połowie swojej długości, zatem wystarczy wyznaczyć środek odcinka \(AC\) (a mamy na to wzór w tablicach).
Zgodnie ze wzorami współrzędne \(S=(x_{S};y_{S})\) środka odcinka \(AC\) możemy obliczyć w następujący sposób:
$$x_{S}=\frac{x_{A}+x_{C}}{2} \\
x_{S}=\frac{-6-2\sqrt{2}+2+6\sqrt{2}}{2} \\
x_{S}=\frac{-4+4\sqrt{2}}{2} \\
x_{S}=-2+2\sqrt{2}$$
Tak naprawdę moglibyśmy w tym momencie skończyć rozwiązywanie zadania, bo tylko w czwartej odpowiedzi znajduje się obliczona przed chwilą współrzędna \(x_{S}\). Dla sprawdzenia i wprawy obliczmy sobie jeszcze współrzędną \(y_{S}\):
$$y_{S}=\frac{y_{A}+y_{C}}{2} \\
y_{S}=\frac{4-2\sqrt{2}+6-2\sqrt{2}}{2} \\
y_{S}=\frac{10-4\sqrt{2}}{2} \\
y_{S}=5-2\sqrt{2}$$
D. \(S=(-2+2\sqrt{2},\;5-2\sqrt{2})\)

