Punkty \(A=(3,3)\) i \(B=(9,1)\) są wierzchołkami trójkąta \(ABC\), a punkt \(M=(1,6)\) jest środkiem boku \(AC\). Oblicz współrzędne punktu przecięcia prostej \(AB\) z wysokością tego trójkąta, poprowadzoną z wierzchołka \(C\).
Zaznaczmy w układzie współrzędnych punkty z treści zadania i od razu oszacujmy mniej więcej gdzie znajdzie się punkt \(C\) (z którego to wierzchołka musimy poprowadzić później wysokość trójkąta) oraz punkt \(D\), którego współrzędnych poszukujemy.
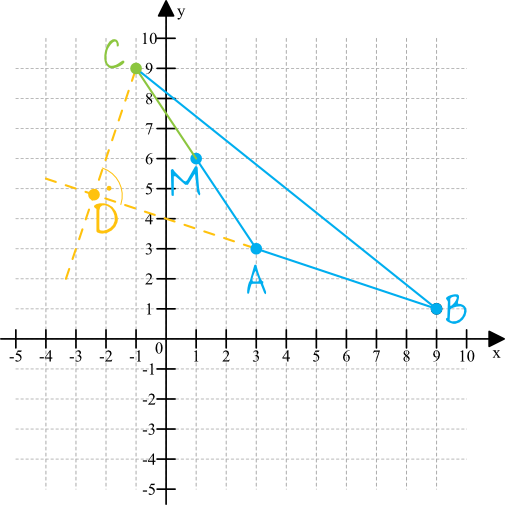
Skorzystamy ze wzoru na środek odcinka \(AC\), bowiem znamy współrzędne środka \(M\) i znamy też współrzędne punktu \(A\), zatem jedyną niewiadomą będą w tej sytuacji współrzędne punktu \(C\). Obliczmy po kolei każdą ze współrzędnych:
$$x_{M}=\frac{x_{A}+x_{C}}{2} \\
1=\frac{3+x_{C}}{2} \\
2=3+x_{C} \\
x_{C}=-1 \\
\text{oraz}\\
y_{M}=\frac{y_{A}+y_{C}}{2} \\
6=\frac{3+y_{C}}{2} \\
12=3+y_{C} \\
y_{C}=9$$
Współrzędne punktu \(C\) to w takim razie \(C=(-1;9)\).
Potrzebujemy znać równanie prostej \(AB\), bo to na jej przedłużeniu znajdzie się poszukiwany przez nas punkt \(D\). Możemy tutaj skorzystać ze wzoru na równanie prostej, zatem:
$$(y-y_{A})(x_{B}-x_{A})-(y_{B}-y_{A})(x-x_{A})=0 \\
(y-3)(9-3)-(1-3)(x-3)=0 \\
(y-3)6-(-2)(x-3)=0 \\
6y-18-(-2x+6)=0 \\
6y-18+2x-6=0 \\
6y+2x-24=0 \\
6y=-2x+24 \\
y=-\frac{2}{6}x+4 \\
y=-\frac{1}{3}x+4$$
Aby dwie proste były względem siebie prostopadłe to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Skoro pierwsza prosta ma \(a=-\frac{1}{3}\), to poszukiwana prosta prostopadła ma na pewno współczynnik kierunkowy równy:
$$-\frac{1}{3}\cdot a=-1 \\
a=3$$
Wiemy już, że nasza prosta prostopadła ma wzór \(y=3x+b\). Musimy jeszcze wyznaczyć współczynnik \(b\), tak aby ta prosta przechodziła dokładnie przez punkt \(C\). Aby to osiągnąć Wystarczy podstawić do tego wzoru współrzędne punktu \(C\) (obliczyliśmy je sobie w drugim kroku):
$$y=3x+b \\
9=3\cdot(-1)+b \\
9=-3+b \\
b=12$$
Poszukiwana prosta prostopadła wyraża się więc wzorem \(y=3x+12\).
Z geometrycznej interpretacji układu równań wiemy, że rozwiązaniem układu równań dwóch prostych jest punkt ich przecięcia się. Tworząc więc układ równań z dwóch prostych (których wzory sobie wyznaczyliśmy w poprzednich krokach) obliczymy poszukiwane współrzędne punktu \(D\).
\begin{cases}
y=-\frac{1}{3}x+4 \\
y=3x+12
\end{cases}
Podstawiając pierwsze równanie do drugiego otrzymamy:
$$-\frac{1}{3}x+4=3x+12 \quad\bigg/\cdot3 \\
-x+12=9x+36 \\
-10x=24 \\
x=-2,4$$
Drugą współrzędną obliczymy podstawiając \(x=-2,4\) do jednego z równań:
$$y=3\cdot(-2,4)+12 \\
y=-7,2+12 \\
y=4,8$$
To oznacza, że współrzędnymi poszukiwanego punktu są \(D=(-2,4;\;4,8)\).
\(D=(-2,4;\;4,8)\)

