Punkty A=(2,11), B=(8,23), C=(6,14) są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka C

Punkty \(A=(2,11)\), \(B=(8,23)\), \(C=(6,14)\) są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka \(C\) przecina prostą \(AB\) w punkcie \(D\). Oblicz współrzędne punktu \(D\).

Naszkicujmy sobie układ współrzędnych i zaznaczmy w nim współrzędne punktów z treści zadania.

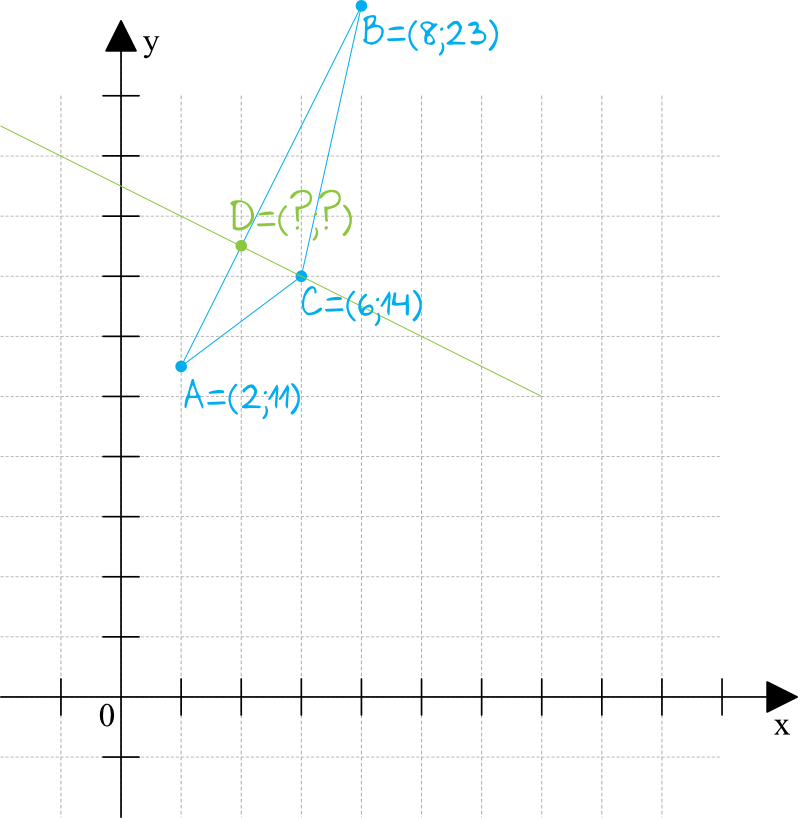
Najlepszą metodą na znalezienie współrzędnych punktu \(D\) będzie chyba wyznaczenie najpierw równania prostej \(AB\), później wyznaczenie równania prostej prostopadłej przechodzącej przez punkt \(C\), no i na sam koniec rozwiązanie układu równań złożonego z tych dwóch prostych.

Do wyznaczenia równania prostej przechodzącej przez punkt \(A=(x_{A};y_{A})\) oraz \(B=(x_{B};y_{B})\) możemy posłużyć się prostym wzorem:
$$(y-y_{A})(x_{B}-x_{A})-(y_{B}-y_{A})(x-x_{A})=0$$

Podstawiając współrzędne punktów \(A=(2,11)\) oraz \(B=(8,23)\) otrzymamy:
$$(y-11)(8-2)-(23-11)(x-2)=0 \\
(y-11)\cdot6-12\cdot(x-2)=0 \\
6y-66-12x+24=0 \\
6y-12x-42=0 \\
6y=12x+42 \quad\bigg/:6 \\
y=2x+7$$

Szukamy prostej prostopadłej w postaci \(y=ax+b\). Aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych \(a\) musi być równy \(-1\). Skoro więc pierwsza prosta ma \(a=2\), to druga musi mieć:
$$a\cdot2=-1 \\
a=-\frac{1}{2}$$

Wiemy już, że nasza prosta prostopadła przyjmuje postać \(y=-\frac{1}{2}x+b\). Aby wyznaczyć brakujący współczynnik \(b\) wystarczy podstawić współrzędne punktu \(C=(6;14)\), który przez tą prostą przechodzi. Otrzymamy wtedy:
$$y=-\frac{1}{2}x+b \\
14=-\frac{1}{2}\cdot6+b \\
14=-3+b \\
b=17$$

To oznacza, że prosta prostopadła ma wzór \(y=-\frac{1}{2}x+17\).

Z interpretacji geometrycznej układu równań wiemy, że rozwiązaniem układu równań składającego się z dwóch prostych są współrzędne punktu przecięcia się tych prostych. W naszym przypadku będą to poszukiwane współrzędne punktu \(D\), zatem:
\begin{cases}
y=2x+7 \\
y=-\frac{1}{2}x+17
\end{cases}

Korzystając z metody podstawiania, możemy podstawić wartość \(y=2x+7\) z pierwszego równania do drugiego, otrzymując:
$$2x+7=-\frac{1}{2}x+17 \quad\bigg/\cdot2 \\
4x+14=-x+34 \\
5x=20 \\
x=4$$

Podstawiając wartość \(x=4\) do jednego z równań obliczymy drugą współrzędną:
$$y=2\cdot4+7 \\
y=8+7 \\
y=15$$

Współrzędne poszukiwanego punktu to w takim razie \(D=(4;15)\).

\(D=(4;15)\)