Punkty A=(-1,-5), B=(3,-1) i C=(2,4) są kolejnymi wierzchołkami równoległoboku ABCD. Oblicz pole tego równoległoboku

Punkty \(A=(-1,-5)\), \(B=(3,-1)\) i \(C=(2,4)\) są kolejnymi wierzchołkami równoległoboku \(ABCD\). Oblicz pole tego równoległoboku.

To zadanie jest chyba jednym z najbardziej rozbudowanych zadań jakie pojawiły się na maturze w ciągu ostatnich lat, zwłaszcza jeśli chcielibyśmy to obliczać standardową metodą. Prześledźmy sobie ten najbardziej typowy tok rozwiązania tego zadania, a ja za chwilę powiem Ci jak można to zadanie zrobić znacznie szybciej.

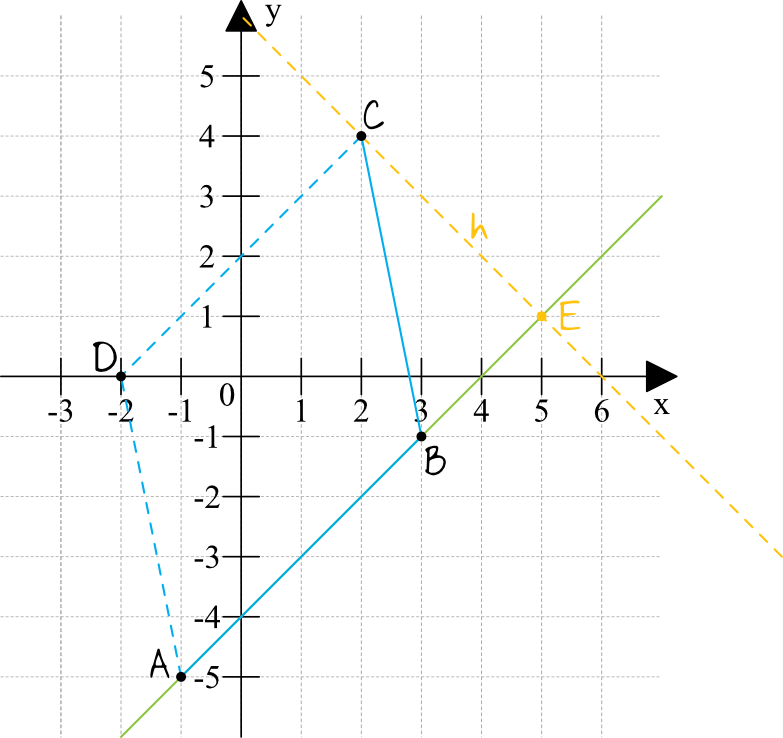
Zaznaczmy sobie w układzie współrzędnych punkty \(A\), \(B\) oraz \(C\). Możemy też sobie mniej lub bardziej dokładnie zaznaczyć punkt \(D\), tak aby wiedzieć jak wygląda ten równoległobok. Nie mniej jednak punkt \(D\) nam nie będzie potrzebny, bo do obliczenia pola powierzchni potrzebujemy znać długość podstawy (czyli \(|AB|\)) oraz wysokość trójkąta. Z tą wysokością problem jest taki, że znajduje się ona poza figurą i chcąc poznać jej długość musimy zaznaczyć sobie nowy punkt \(E\), którego współrzędnych nie znamy. O punkcie \(E\) Wiemy tylko tyle, że leży na pewno na przedłużeniu odcinka \(AB\) i to pozwoli nam wyznaczyć jego współrzędne. Ogólnie proces liczenia będzie bardzo długi i żmudny:
– musimy wyznaczyć wzór prostej przechodzącej przed punkty \(A\) i \(B\) (ze wzoru lub z układu równań)
– musimy wyznaczyć wzór prostej prostopadłej, która przejdzie przez punkt \(C\)
– na przecięciu się tych dwóch prostych znajdzie się ten problematyczny punkt \(E\) (rozwiązując układ równań poznamy jego współrzędne)
– musimy obliczyć długość odcinka \(AB\)
– musimy obliczyć długość odcinka \(CE\)
– no i na koniec musimy wymnożyć wartości długości tych dwóch odcinków obliczając tym samym pole

Rozwiązywanie tego w ten sposób zajmie naprawdę dużo czasu, a i o pomyłkę będzie dość prosto. Awaryjnie można też byłoby skorzystać ze wzoru na odległość punktu od prostej, dzięki czemu moglibyśmy pominąć obliczenie współrzędnych punktu \(E\). Wtedy podstawilibyśmy do tego wzoru współrzędne punktu \(C\) oraz wzór prostej przechodzącej przez odcinek \(AB\).

Teoretycznie można byłoby się też pokusić o pewne uproszczenie, wyznaczając długości odcinków \(AB\) oraz \(CE\) z Twierdzenia Pitagorasa i licząc po kratkach poszczególne długości przyprostokątnych.

Wszystkie problemy jednak znikają kiedy dostrzeżemy, że wystarczyłoby obliczyć pole trójkąta \(ABC\) i pomnożyć tą wartość przez \(2\), wszak przekątna równoległoboku dzieli figurę na dwa trójkąty o równej powierzchni. I już za sam fakt dostrzeżenia tego można było na maturze otrzymać jeden punkt. Pytanie tylko jak wyliczyć pole tego trójkąta. I tu z pomocą przychodzi nam wzór z tablic, o którym mało kto wie, bo jest bardzo rzadko stosowany.

W tablicach odczytujemy wzór na pole trójkąta, znając współrzędne wszystkich trzech punktów:
Pole trójkąta \(ABC\) o znanych współrzędnych wierzchołków wyliczymy z następującego wzoru:
$$P=\frac{1}{2}\cdot|(x_{B}-x_{A})(y_{C}-y_{A})-(y_{B}-y_{A})(x_{C}-x_{A})|$$

Podstawiając odpowiednie współrzędne otrzymamy:
$$P=\frac{1}{2}\cdot|(3-(-1))(4-(-5))-(-1-(-5))(2-(-1))| \\
P=\frac{1}{2}\cdot|4\cdot9-4\cdot3| \\
P=\frac{1}{2}\cdot|36-12| \\
P=\frac{1}{2}\cdot24 \\
P=12$$

Zgodnie z tym co sobie powiedzieliśmy, przekątna \(AC\) dzieli równoległobok na dwa równe trójkąty, tak więc skoro znamy pole trójkąta \(ABC\) to wystarczy teraz wynik ten pomnożyć przez \(2\) i otrzymamy pole równoległoboku:
$$P=2\cdot12 \\
P=24$$

\(P=24\)