Punkty \(A=(1,5)\), \(B=(14,31)\), \(C=(4,31)\) są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka \(C\) przecina prostą \(AB\) w punkcie \(D\). Oblicz długość odcinka \(BD\).
Nie musimy dokładnie zaznaczać wszystkiego na układzie współrzędnych, ale dobrze jest chociaż poglądowo narysować sobie ułożenie tego trójkąta, dzięki czemu łatwiej nam będzie wykonać późniejsze obliczenia.
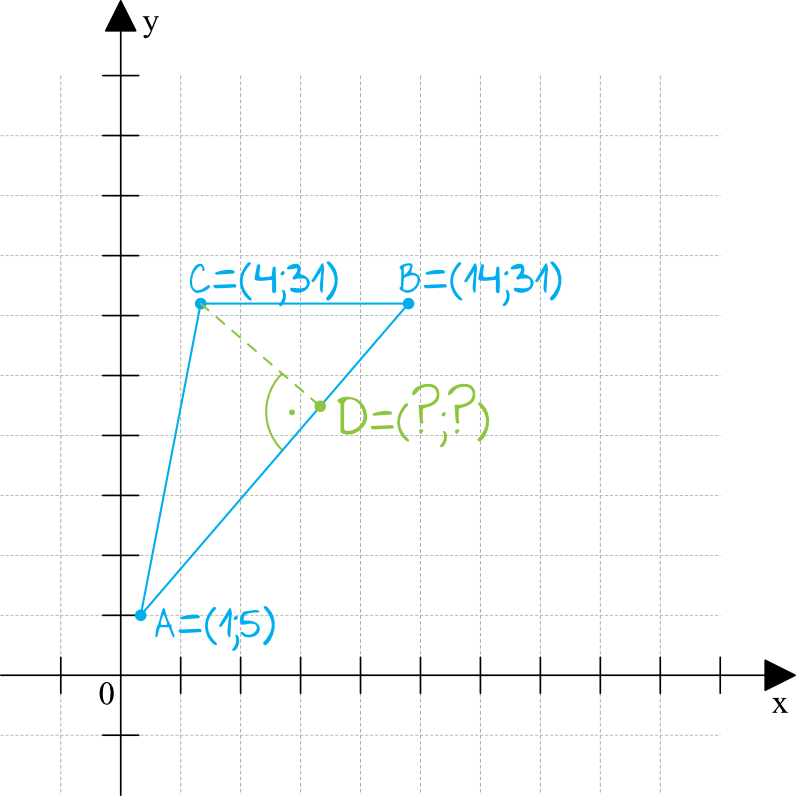
Znamy współrzędne punktów \(A\), \(B\) oraz \(C\), więc za pomocą wzoru moglibyśmy obliczyć równanie każdej prostej, która przechodzi przez dwa wybrane przez nas punkty. Gdybyśmy znali wzory prostych \(AB\) oraz \(CD\) i stworzyli z nich układ równań, to wynik jaki byśmy otrzymali byłby punktem przecięcia się tych prostych, a więc byłyby to współrzędne punktu \(D\), którego nam brakuje.
Ustalmy więc teraz jak wyznaczyć wzory prostych \(AB\) oraz \(CD\).
• Wzór na prostą \(AB\) wyznaczymy tworząc bardzo prosty układ równań składający się z dwóch równań funkcji \(y=ax+b\), gdzie w pierwszym równaniu za \(x\) oraz \(y\) podstawimy współrzędne punktu \(A\), a w drugim równaniu współrzędne punktu \(B\). Ewentualnie moglibyśmy skorzystać ze wzoru na równanie prostej przechodzącej przez dwa punkty, który znajduje się w tablicach.
• Wzór na prostą \(CD\) wyznaczymy korzystając z tego, że jest to prosta prostopadła do prostej \(AB\), a więc iloczyn współczynników prostych \(CD\) oraz \(AB\) będzie musiał być równy \(-1\).
Po ustaleniu współrzędnych punktu \(D\) bez problemu obliczymy długość odcinka \(BD\) ze wzoru:
$$|BD|=\sqrt{(x_{D}-x_{B})^2+(y_{D}-y_{B})^2}$$
Teraz czas na obliczenia tych elementów, które wypisaliśmy sobie w naszym planie działania.
Pod ogólny wzór funkcji \(y=ax+b\) podstawiamy współrzędne punktu \(A\) oraz \(B\), tworząc układ równań:
\begin{cases}
5=a+b \\
31=14a+b
\end{cases}
Aby rozwiązać ten układ równań najprościej jest odjąć pierwsze równanie od drugiego, albo też do drugiego równania podstawić wartość \(b=5-a\) wynikającą z pierwszego równania. W obydwu przypadkach dojdziemy do tego, że \(13a=26\), więc \(a=2\).
Bez problemu wyliczymy także współczynnik \(b\), korzystając chociażby z równania \(b=5-a\), a więc \(b=5-2=3\).
Wyszło nam, że wzór funkcji przechodzącej przez nasze punkty \(A\) oraz \(B\) to \(y=2x+3\).
Ustaliliśmy już, że prosta \(CD\) będzie prostopadła do prostej \(AB\). To oznacza, że iloczyn ich współczynników \(a\) będzie równy \(-1\). Skoro współczynnik \(a\) prostej \(AB\) był równy \(2\), to współczynnik \(a\) prostej \(CD\) będzie równy:
$$a\cdot2=-1 \\
a=-\frac{1}{2}$$
Wzór prostej \(CD\) ma więc postać \(y=-\frac{1}{2}x+b\).
Musimy jeszcze obliczyć współczynnik \(b\), a zrobimy to podstawiając do wzoru funkcji współrzędne punktu \(C=(4,31)\), stąd też:
$$31=-\frac{1}{2}\cdot4+b \\
31=-2+b \\
b=33$$
W związku z tym prosta \(CD\) wyraża się równaniem \(y=-\frac{1}{2}x+33\).
Musimy teraz wyznaczyć współrzędne punktu \(D\), a zrobimy to korzystając z tego, że proste \(AB\) oraz \(BD\) przecinają się w punkcie \(D\). Współrzędne punktu \(D\) otrzymamy więc rozwiązując prosty układ równań, który składa się z równań prostych \(AB\) oraz \(CD\):
\begin{cases}
y=2x+3 \\
y=-\frac{1}{2}x+33
\end{cases}
Metodą podstawiania podstawiamy za \(y\) wartość z pierwszego równania do drugiego i otrzymujemy równanie:
$$2x+3=-\frac{1}{2}x+33 \\
2\frac{1}{2}x=30 \\
x=12$$
Obliczmy jeszcze współrzędną \(y\):
$$y=2x+3 \\
y=2\cdot12+3 \\
y=27$$
W ten sposób wyznaczyliśmy współrzędne punktu \(D=(12;27)\).
Z tablic maturalnych możemy odczytać wzór na długość odcinka (a w zasadzie na odległość między dwoma punktami), dzięki któremu po podstawieniu odpowiednich współrzędnych wyznaczymy długość odcinka \(BD\):
$$|BD|=\sqrt{(x_{D}-x_{B})^2+(y_{D}-y_{B})^2} \\
|BD|=\sqrt{(12-14)^2+(27-31)^2} \\
|BD|=\sqrt{4+16} \\
|BD|=\sqrt{20} \\
|BD|=2\sqrt{5}$$
\(|BD|=2\sqrt{5}\)

