Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy nanieść na układ współrzędnych znane nam punkty oraz równanie prostej \(AB\), tak aby łatwiej dostrzec co musimy policzyć:
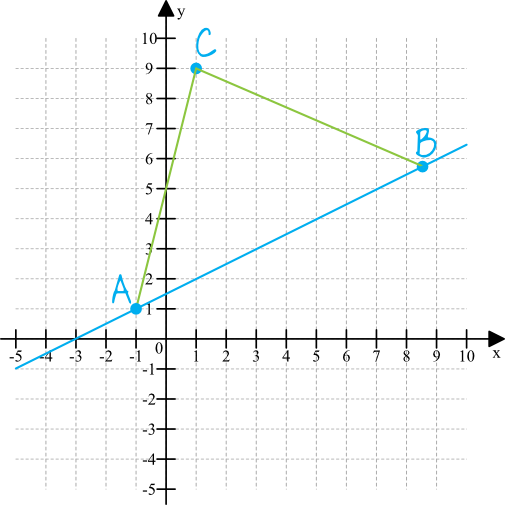
Krok 2. Ułożenie i rozwiązanie równania.
Z treści zadania wynika, że boku \(AC\) oraz \(BC\) są równej długości. Możemy więc skorzystać ze wzoru na długość odcinka w układzie współrzędnych \(|AC|=\sqrt{(x_{C}-x_{A})^2+(y_{C}-y_{A})^2}\) oraz \(|BC|=\sqrt{(x_{C}-x_{B})^2+(y_{C}-y_{B})^2}\) i podstawić tam współrzędne naszych punktów \(A=(-1,1)\), \(C=(1,9)\) oraz \(B=(x,y)\). Otrzymamy wtedy:
$$\sqrt{(x_{C}-x_{A})^2+(y_{C}-y_{A})^2}=\sqrt{(x_{C}-x_{B})^2+(y_{C}-y_{B})^2} \\
\sqrt{(1-(-1))^2+(9-1)^2}=\sqrt{(1-x)^2+(9-y)^2} \quad\bigg/^2 \\
(1+1)^2+(9-1)^2=(1-x)^2+(9-y)^2 \\
2^2+8^2=(1-x)^2+(9-y)^2 \\
4+64=(1-x)^2+(9-y)^2 \\
(1-x)^2+(9-y)^2=68$$
Krok 3. Doprowadzenie do równania z jedną niewiadomą.
Póki co mamy równanie z dwiema niewiadomymi - \(x\) oraz \(y\). Pod wartość igreka możemy teraz podstawić równanie z treści zadania, czyli \(y=\frac{1}{2}x+\frac{3}{2}\). Dzięki temu będziemy mieć równanie z jedną niewiadomą. I ten sposób rozwiązania jest dobry (i jest chyba najpopularniejszy), ale sprawi iż w trakcie liczenia będziemy mieć dużo ułamków na swojej drodze, przez co łatwo będzie o błąd. Możemy więc postąpić nieco sprytniej. Przekształcając równanie prostej otrzymamy:
$$y=\frac{1}{2}x+\frac{3}{2} \quad\bigg/\cdot2 \\
2y=x+3 \\
x=2y-3$$
Teraz możemy podstawić to równanie pod naszego iksa i otrzymamy:
$$(1-(2y-3))^2+(9-y)^2=68 \\
(1-2y+3)^2+(9-y)^2=68 \\
(4-2y)^2+(9-y)^2=68 \\
16-16y+4y^2+81-18y+y^2=68 \\
5y^2-34y+97=68 \\
5y^2-34y+29=0$$
Krok 4. Rozwiązanie powstałego równania kwadratowego.
Powstało nam równanie kwadratowe, zatem:
Współczynniki: \(a=5,\;b=-34,\;c=29\)
$$Δ=b^2-4ac=(-34)^2-4\cdot5\cdot29=1156-580=576 \\
\sqrt{Δ}=\sqrt{576}=24$$
$$y_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-34)-24}{2\cdot5}=\frac{34-24}{10}=\frac{10}{10}=1 \\
y_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-34)+24}{2\cdot5}=\frac{34+24}{10}=\frac{58}{10}=\frac{29}{5}$$
Krok 5. Interpretacja otrzymanego wyniku i wyznaczenie współrzędnych punktu \(B\).
Otrzymaliśmy dwa wyniki: \(y=1\) oraz \(y=\frac{29}{5}\). Spróbujmy zatem wyznaczyć dla obu tych przypadków współrzędną iksową, podstawiając igreki np. do równania \(x=2y-3\).
Dla \(y=1\):
$$x=2\cdot1-3 \\
x=2-3 \\
x=-1$$
Otrzymaliśmy zatem współrzędne \(x=-1\) oraz \(y=1\), czyli współrzędne punktu \(A\).
Dla \(y=\frac{29}{5}\):
$$x=2\cdot\frac{29}{5}-3 \\
x=\frac{58}{5}-3 \\
x=\frac{43}{5}$$
Otrzymaliśmy zatem współrzędne \(x=\frac{43}{5}\) oraz \(y=\frac{29}{5}\) i to są właśnie współrzędne punktu \(B\).