Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zakładając, że odcinek \(SB\) ma długość \(x\), to nasz bok \(AD\) będzie mieć długość \(2x\). Dodatkowo warto zauważyć, że trójkąt \(ADS\) jest równoramienny, którego dwa ramiona mają długość po \(5cm\).
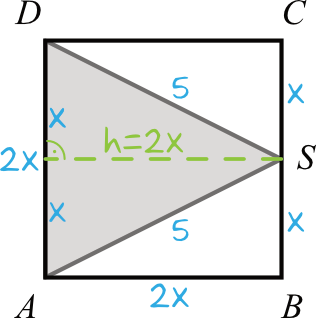
Do obliczenia obwodu brakuje nam długości długości podstawy trójkąta, czyli długości boku \(AD\).
Krok 2. Obliczenie długości podstawy trójkąta \(ADS\).
Wysokość dzieli nam podstawę trójkąta na dwie równe części i właśnie to pozwoli nam obliczyć brakującą długość odcinka \(AD\). Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$x^2+(2x)^2=5^2 \\
x^2+4x^2=25 \\
5x^2=25 \\
x^2=5 \\
x=\sqrt{5} \quad\lor\quad x=-\sqrt{5}$$
Ujemną długość oczywiście odrzucamy, zatem zostaje nam \(x=\sqrt{5}\).
Podstawa \(AD\) ma długość \(2x\), zatem będzie ona mieć długość \(|AD|=2\sqrt{5}cm\).
Krok 3. Obliczenie długości obwodu.
Na koniec została już tylko formalność, czyli obliczenie obwodu. Dodając do siebie długości wszystkich boków trójkąta \(ADS\) otrzymamy:
$$5cm+5cm+2\sqrt{5}cm=(10+2\sqrt{5})cm$$