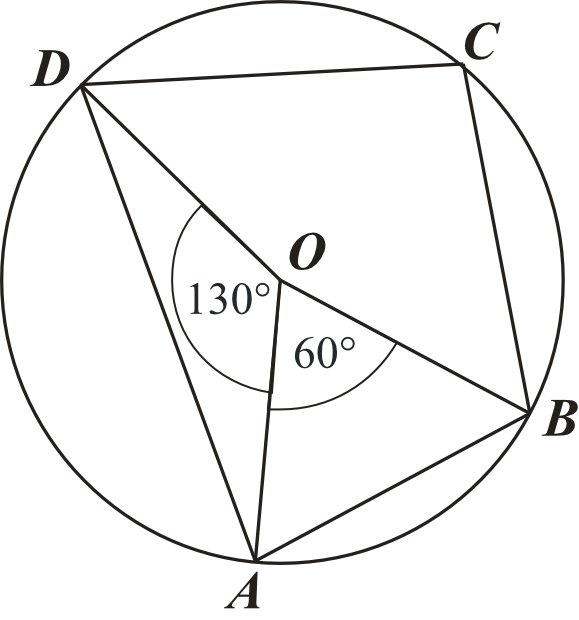
Punkt \(O\) jest środkiem okręgu. Kąt wpisany \(BAD\) ma miarę:
\(150°\)
\(120°\)
\(115°\)
\(85°\)
Rozwiązanie:
Aby móc skorzystać z twierdzenia o kątach środkowych i wpisanych opartych na tym samym łuku potrzebujemy znać miarę kąta \(DOB\), bo to właśnie kąt środkowy \(DOB\) jest oparty na tym samym łuku co poszukiwany kąt \(BAD\).
Krok 1. Obliczenie miary kąta środkowego \(DOB\).
Skoro kąt pełny ma miarę \(360°\), to:
$$|\sphericalangle DOB|=360°-130°-60°=170°$$
Krok 2. Obliczenie miary kąta wpisanego \(BAD\).
Kąt wpisany na okręgu ma miarę dwa razy mniejszą od kąta środkowego opartego na tym samym łuku. Zatem:
$$|\sphericalangle BAD|=170°:2=85°$$
Odpowiedź:
D. \(85°\)

