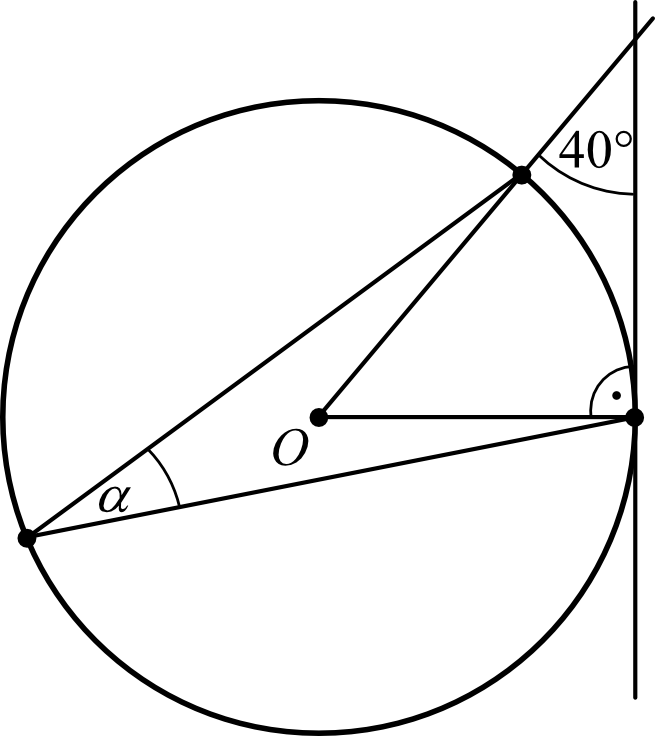
Punkt O jest środkiem okręgu. Kąt alfa, zaznaczony na rysunku, ma miarę

Punkt \(O\) jest środkiem okręgu. Kąt \(α\), zaznaczony na rysunku, ma miarę:

Musimy obliczyć miarę kąta środkowego przy punkcie \(O\). Skorzystamy tutaj z trójkąta, którego miary dwóch kątów są tak naprawdę podane, to \(40°\) oraz \(90°\). Oznaczmy więc sobie trzeci kąt tego trójkąta jako \(β\) (patrz rysunek).

Skoro suma kątów w trójkącie jest równa \(180°\), to:
$$β=180°-40°-90° \\
β=50°$$

Kąt wpisany ma dwa razy mniejszą miarę od kąta środkowego opartego na tym samym łuku, zatem:
$$α=50°:2=25°$$

C. \(25°\)