Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Z treści zadania wynika, że trójkąt jest równoramienny i że ramionami są boki \(KM\) oraz \(LM\). Musimy więc wprowadzić poprawne oznaczenia punktów do naszego trójkąta, tak aby móc potem z rysunku wyciągnąć odpowiednie wnioski. Całość będzie wyglądać mniej więcej w ten sposób:
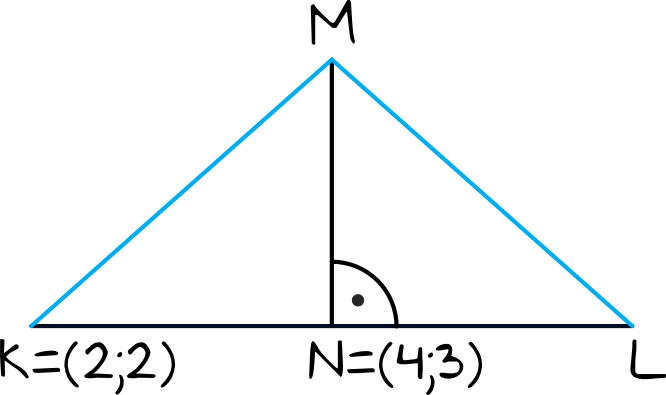
Krok 2. Obliczenie współrzędnych punktu \(L\).
Z rysunku wynika, że punkt \(N\) jest środkiem odcinka \(KL\). Skoro znamy współrzędne punktu \(K\) oraz \(N\), to jesteśmy w stanie obliczyć współrzędne punktu \(L\) korzystając ze wzoru na środek odcinka:
$$N=\left(\frac{x_{K}+x_{L}}{2};\frac{y_{K}+y_{L}}{2}\right)$$
Dla przejrzystości obliczeń wyznaczmy każdą ze współrzędnych oddzielnie:
$$x_{N}=\frac{x_{K}+x_{L}}{2} \\
4=\frac{2+x_{L}}{2} \\
8=2+x_{L} \\
x_{L}=6 \\
\quad \\
y_{N}=\frac{y_{K}+y_{L}}{2} \\
3=\frac{2+y_{L}}{2} \\
6=2+y_{L} \\
y_{L}=4$$