Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania wygląda następująco:
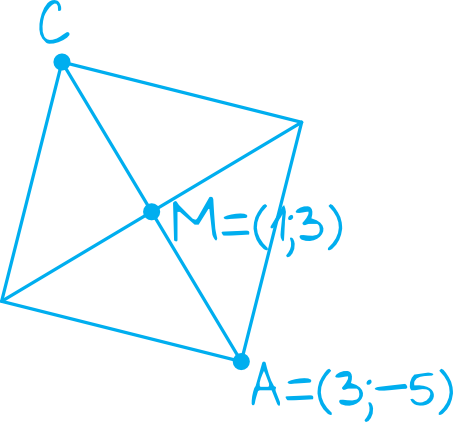
Krok 2. Obliczenie długości odcinka \(AM\).
Korzystając ze wzoru na długość odcinka, możemy zapisać, że:
$$|AM|=\sqrt{(x_{M}-x_{A})^2+(y_{M}-y_{A})^2} \\
|AM|=\sqrt{(1-3)^2+(3-(-5))^2} \\
|AM|=\sqrt{(-2)^2+8^2} \\
|AM|=\sqrt{4+64} \\
|AM|=\sqrt{68}$$
Krok 3. Obliczenie długości przekątnej kwadratu.
Odcinek \(|AM|\) stanowi połowę długości przekątnej, zatem:
$$d=2\sqrt{68}$$
Krok 4. Obliczenie pola kwadratu.
Możemy oczywiście obliczyć długość boku kwadratu i tym samym skorzystać później ze wzoru \(P=a^2\). Warto jednak pamiętać, że pole kwadratu damy radę także obliczyć ze wzoru:
$$P=\frac{1}{2}\cdot d^2 \\
P=\frac{1}{2}\cdot(2\sqrt{68})^2 \\
P=\frac{1}{2}\cdot4\cdot68 \\
P=136$$