Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Z treści zadania wynika, że trójkąt \(ABC\) jest równoramienny, bo boki \(AC\) oraz \(BC\) mają jednakową długość. Nanosząc dane z treści zadania otrzymamy taką oto sytuację:
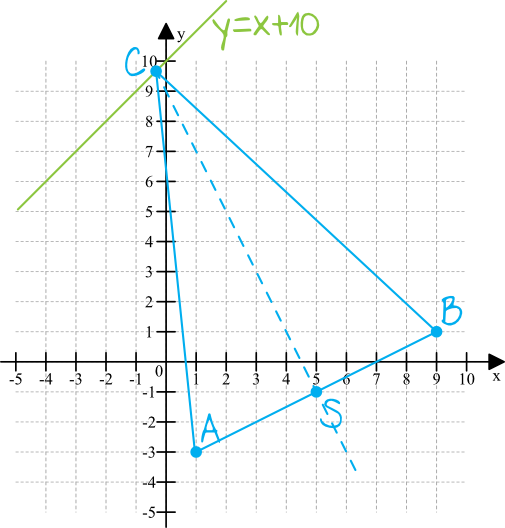
Krok 2. Obliczenie współrzędnych punktu \(B\).
Środek odcinka \(AB\) o współrzędnych \(A=(x_{A};y_{A})\) oraz \(B=(x_{B};y_{B})\) możemy opisać wzorem:
$$S=\left(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2}\right)$$
Znamy współrzędne punktu \(A=(1,-3)\) oraz środek odcinka \(AB\), czyli \(S=(5,-1)\). W związku z tym bez problemy możemy obliczyć współrzędne punktu \(B\). Dla przejrzystości zapisu obliczmy każdą ze współrzędnych oddzielnie:
$$x_{S}=\frac{x_{A}+x_{B}}{2} \\
5=\frac{1+x_{B}}{2} \\
10=1+x_{B} \\
x_{B}=9 \\
\quad \\
y_{S}=\frac{y_{A}+y_{B}}{2} \\
-1=\frac{-3+y_{B}}{2} \\
-2=-3+y_{B} \\
y_{B}=1$$
To oznacza, że \(B=(9;1)\).
Krok 3. Wyznaczenie współczynnika kierunkowego \(a\) prostej \(AB\).
Chcemy wyznaczyć współczynnik kierunkowy \(a\) prostej \(AB\), aby za chwilę móc wyznaczyć równanie prostej prostopadłej przechodzącej przez punkt \(S\). Znamy współrzędne punktów \(A\) oraz \(B\), więc możemy nawet wyznaczyć równanie prostej \(AB\) (korzystając albo z długiego wzoru z tablic, albo z metody układu równań). Skoro jednak nam potrzebny jest tylko współczynnik kierunkowy \(a\), to możemy posłużyć się sprytnym wzorem:
$$a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}$$
Podstawiając współrzędne punktów \(A=(1,-3)\) oraz \(B=(9;1)\), otrzymamy:
$$a=\frac{1-(-3)}{9-1} \\
a=\frac{4}{8} \\
a=\frac{1}{2}$$
Krok 4. Wyznaczenie równania prostej \(SC\).
Z rysunku wynika, że chcąc wyznaczyć współrzędne punktu \(C\), musimy najpierw wyznaczyć prostą prostopadłą do prostej \(AB\), która przechodzi przez punkt \(S=(5,-1)\). Aby dwie proste były względem siebie prostopadłe, iloczyn ich współczynników kierunkowych musi być równy \(-1\). W poprzednim kroku ustaliliśmy już, że prosta \(AB\) ma współczynnik \(a=\frac{1}{2}\), więc prosta prostopadła będzie mieć współczynnik \(a=-2\), bo \(\frac{1}{2}\cdot(-2)=-1\). To oznacza, że prostą prostopadłą możemy zapisać jako \(y=-2x+b\).
Do pełnego równania prostej prostopadłej brakuje nam jeszcze współczynnika \(b\). Chcemy, by prosta prostopadła przechodziła przez punkt \(S=(5,-1)\), zatem podstawiając \(x=5\) oraz \(y=-1\) do równania \(y=-2x+b\), otrzymamy:
$$-1=-2\cdot5+b \\
-1=-10+b \\
b=9$$
To oznacza, że interesująca nas prosta prostopadła (pokrywająca się z wysokością trójkąta \(ABC\)) wyraża się równaniem \(y=-2x+9\).
Krok 5. Wyznaczenie współrzędnych punktu \(C\).
Punkt \(C\) jest miejscem przecięcia się prostych prostopadłych określonych równaniami \(y=x+10\) oraz \(y=-2x+9\). Z geometrycznej interpretacji układu równań wiemy, że współrzędne tego punktu wyznaczymy rozwiązując następujący układ równań:
\begin{cases}
y=x+10 \\
y=-2x+9
\end{cases}
Korzystając z metody podstawiania wyjdzie nam, że:
$$x+10=-2x+9 \\
3x=-1 \\
x=-\frac{1}{3}$$
Pierwszą współrzędną punktu \(C\) już więc znamy. Współrzędną \(y\) obliczymy podstawiając \(x=-\frac{1}{3}\) do jednego z równań z układu, np. do pierwszego \(y=x+10\), czyli:
$$y=-\frac{1}{3}+10 \\
y=9\frac{2}{3}$$
To oznacza, że \(C=\left(-\frac{1}{3};9\frac{2}{3}\right)\).