Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
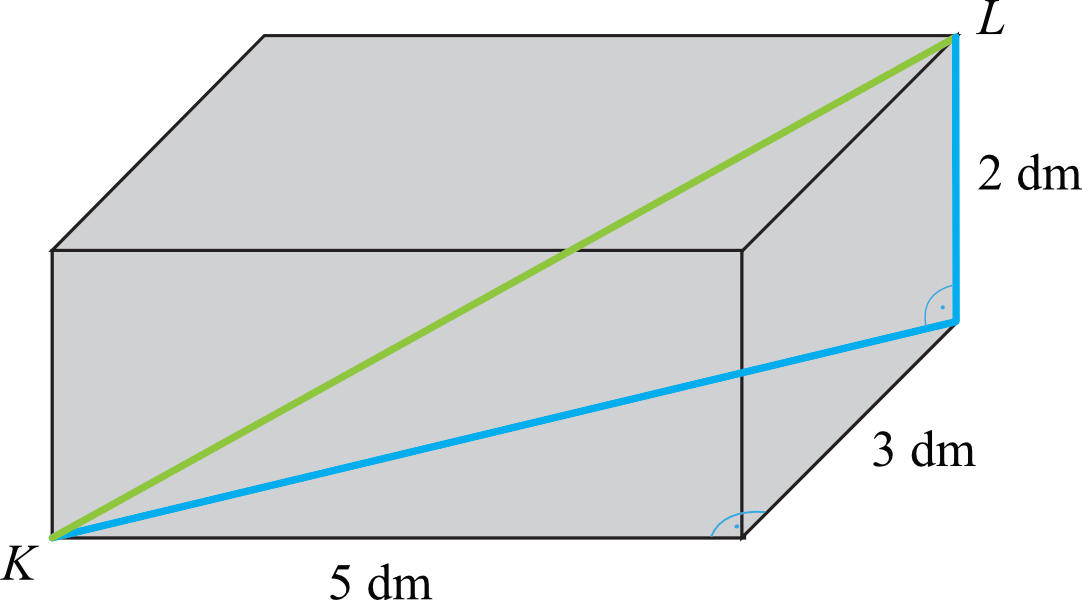
Krok 2. Obliczenie długości przekątnej podstawy.
Zanim obliczymy długość przekątnej \(KL\) to musimy obliczyć długość przekątnej podstawy tego prostopadłościanu. W podstawie mamy prostokąt o bokach \(5dm\) oraz \(3dm\), zatem korzystając z Twierdzenia Pitagorasa otrzymamy:
$$5^2+3^2=c^2 \\
25+9=c^2 \\
c^2=34 \\
c=\sqrt{34} \quad\lor\quad c=-\sqrt{34}$$
Wartość ujemną oczywiście odrzucamy, bo bok nie może mieć ujemnej długości, zatem przekątna podstawy ma długość \(\sqrt{34}dm\).
Krok 3. Obliczenie przekątnej \(KL\).
Przekątna podstawy (którą policzyliśmy przed chwilą), wysokość prostopadłościanu (która ma długość \(2dm\)) oraz przekątna \(KL\) (której szukamy) tworzą trójkąt prostokątny. Zatem ponownie korzystając z Twierdzenia Pitagorasa otrzymamy:
$$(\sqrt{34})^2+2^2=|KL|^2 \\
34+4=|KL|^2 \\
|KL|^2=38 \\
|KL|=\sqrt{38} \quad\lor\quad |KL|=-\sqrt{38}$$
Tutaj ponownie ujemną wartość odrzucamy. Otrzymaliśmy więc informację, że odcinek \(KL\) ma długość \(\sqrt{38}dm\), czyli w przybliżeniu będzie to \(6,16dm\).