Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Przekształcenia wykresów funkcji. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Funkcja \(g(x)\) powstała w wyniku przesunięcia funkcji \(f(x)\) o \(3\) jednostki w dół. W związku z tym:
Zadanie 2. (1pkt) Funkcja \(h(x)\) powstała w wyniku przesunięcia funkcji \(f(x)\) o \(3\) jednostki w lewo. W związku z tym:
Zadanie 3. (1pkt) Funkcję \(f(x)=3x-1\) przesunięto o \(2\) jednostki w prawo. Otrzymana funkcja \(g(x)\) wyraża się wzorem:
Zadanie 4. (1pkt) 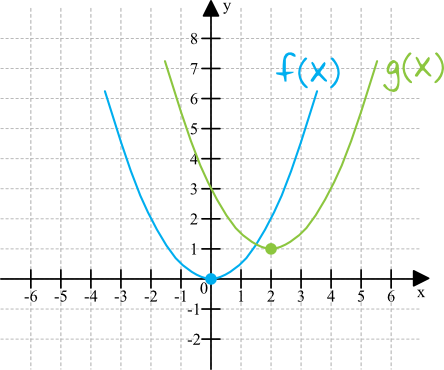
Wzorem funkcji \(g(x)\) jest:
Zadanie 5. (1pkt) Dana jest funkcja liniowa \(f(x)=-2x+4\). Funkcja \(g(x)\) powstała w wyniku symetrii względem osi \(OY\). Co jest prawdą na temat funkcji \(g(x)\)?
Zadanie 6. (1pkt) Funkcje \(f(x)=2x^2-3x+5\) oraz \(g(x)=-2x^2+3x-5\) są swoim odbiciem lustrzanym względem osi iksów.
Zadanie 7. (1pkt) Miejscem zerowym rosnącej funkcji liniowej \(f(x)\) jest \(x=4\). W związku z tym miejscem zerowym funkcji \(g(x)=f(x+5)\) będzie \(x=9\):
Zadanie 8. (1pkt) Zdaniem Jasia chcąc otrzymać wykres funkcji \(g(x)=-3(x-4)^2\) należy przesunąć wykres funkcji \(f(x)=-3x^2\) o \(4\) jednostki w prawo. Małgosia twierdzi, że pomysł Jasia jest błędny i jej zdaniem trzeba byłoby przesunąć wykres funkcji \(f(x)=x^2\) o \(4\) jednostki w prawo i \(3\) jednostki w dół. Kto ma rację?
Zadanie 9. (1pkt) Funkcja kwadratowa \(f(x)\) przyjmuje wartości dodatnie w przedziale \((-3;1)\). W jakim przedziale przyjmuje wartości dodatnie funkcja \(g(x)=-f(x+3)\)?
Zadanie 10. (1pkt) Największa wartość pewnej funkcji kwadratowej \(f(x)\) jest równa \(4\). W związku z tym największą wartością funkcji \(g(x)=f(x-3)\) będzie:
