Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
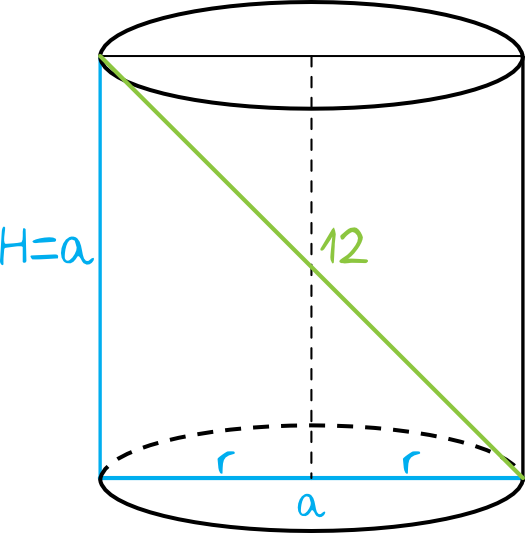
Krok 2. Obliczenie długości boku kwadratu.
Kwadrat o boku \(a\) ma długość przekątnej równą \(a\sqrt{2}\). Skoro nasza przekątna ma długość \(12\), to znaczy że:
$$a\sqrt{2}=12 \\
a=\frac{12}{\sqrt{2}} \\
a=\frac{12\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
a=\frac{12\sqrt{2}}{2} \\
a=6\sqrt{2}$$
Krok 3. Obliczenie długości promienia podstawy.
W podstawie znajduje się koło, którego średnica (zgodnie z rysunkiem) jest równa \(6\sqrt{2}\). Nam do obliczenia objętości będzie potrzebny promień tego koła, a skoro promień jest dwa razy krótszy od średnicy to:
$$r=6\sqrt{2}:2 \\
r=3\sqrt{2}$$
Krok 4. Obliczenie objętości walca.
Wiemy już, że \(r=3\sqrt{2}\). Z rysunku widzimy też, że wysokość walca jest równa długości boku kwadratu, czyli \(H=6\sqrt{2}\), zatem:
$$V=π r^2 \cdot H \\
V=(3\sqrt{2})^2\cdot π\cdot6\sqrt{2} \\
V=9\cdot2\cdot π\cdot6\sqrt{2} \\
V=108\sqrt{2}π$$