Przekątne równoległoboku mają długości \(4\) i \(8\), a kąt między tymi przekątnymi ma miarę \(30°\). Pole tego równoległoboku jest równe:
W tym zadaniu wykorzystamy wzór, który możemy znaleźć w tablicach matematycznych, a mianowicie \(P=\frac{1}{2}\cdot|AC|\cdot|BD|\cdot sinγ\), gdzie \(|AC|\) oraz \(|BD|\) to przekątne równoległoboku, a \(γ\) to kąt między tymi przekątnymi.
I tu ważna uwaga – niektórzy omyłkowo biorą do obliczeń podobny i znacznie popularniejszy wzór (także znajdujący się w tablicach): \(P=a\cdot b\cdot sinα\). Z tego wzoru skorzystać nie możemy, bo w tym wzorze kąt \(α\) to kąt między dwoma bokami równoległoboku, a my znamy kąt między przekątnymi! To główna pułapka w tym zadaniu. Oto wycinek z tablic matematycznych i zaznaczony wzór z którego musimy skorzystać:
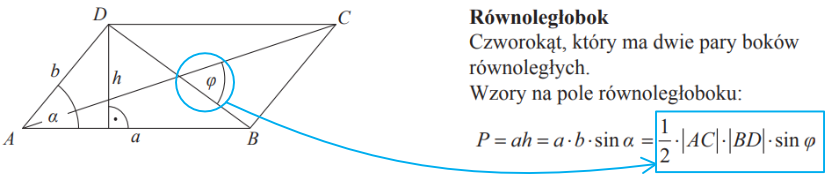
Przechodząc do obliczeń otrzymamy:
$$P=\frac{1}{2}\cdot4\cdot8\cdot sin30° \\
P=16\cdot\frac{1}{2} \\
P=8$$
D. \(8\)

