Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy sobie zwizualizować jak będzie wyglądać nasz trójkąt równoboczny i jak rozkładają się poszczególne miary kątów:
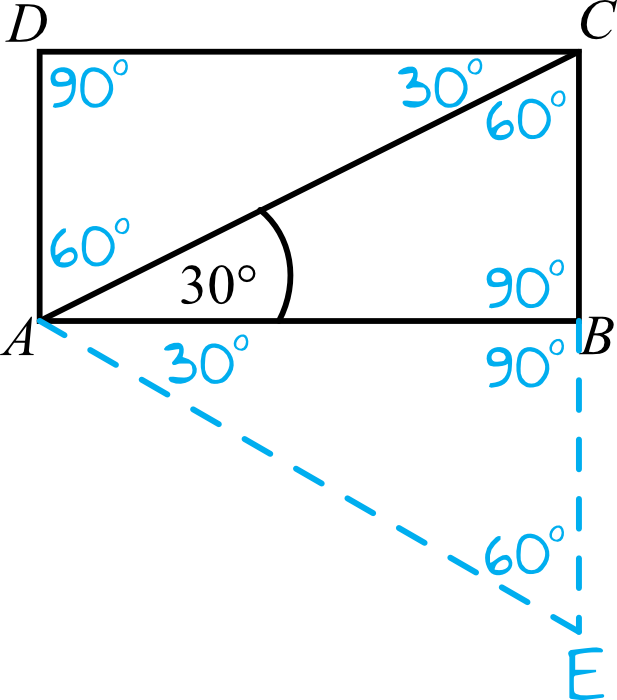
Naszym zadaniem jest udowodnienie, że pole prostokąta \(ABCD\) jest równe polu trójkąta \(ACE\).
Krok 2. Dostrzeżenie trójkątów przystających i zakończenie dowodzenia.
Spójrzmy najpierw na prostokąt \(ABCD\). Pole naszego prostokąta \(ABCD\) składa się z pól dwóch trójkątów: \(ABC\) oraz \(ACD\). Wiemy też, że te dwa trójkąty są trójkątami przystającymi (czyli takimi które mają jednakowe miary i tym samym jednakowe pole powierzchni), bo przekątna dzieli zawsze prostokąt na dwie równe części.
Teraz spójrzmy na trójkąt \(ACE\), który jest naszym trójkątem równobocznym. Tutaj także mamy dwa trójkąty przystające, tym razem \(ABC\) oraz \(ABE\) i suma tych dwóch trójkątów daje pole dużego trójkąta równobocznego.
Skoro więc trójkąt \(ABC\) jest trójkątem przystającym do \(ACD\) oraz \(ABE\), to znaczy że te dwa trójkąty (\(ACD\) oraz \(ABE\)) są także przystające względem siebie i mają jednakowe pole powierzchni. To sprawia, że możemy zakończyć dowodzenie, bo udowodniliśmy że pole zarówno prostokąta jak i trójkąta równobocznego składa się z dwóch trójkątów o identycznych polach powierzchni.