Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Ostrosłup jest czworokątny prawidłowy, zatem w podstawie na pewno znajduje się kwadrat. Jeżeli wysokość ostrosłupa oznaczymy sobie jako \(x\), a przekątną podstawy oznaczymy sobie jako \(2x\) (bo ma być dwa razy dłuższa od przekątnej), to otrzymamy taką oto sytuację:
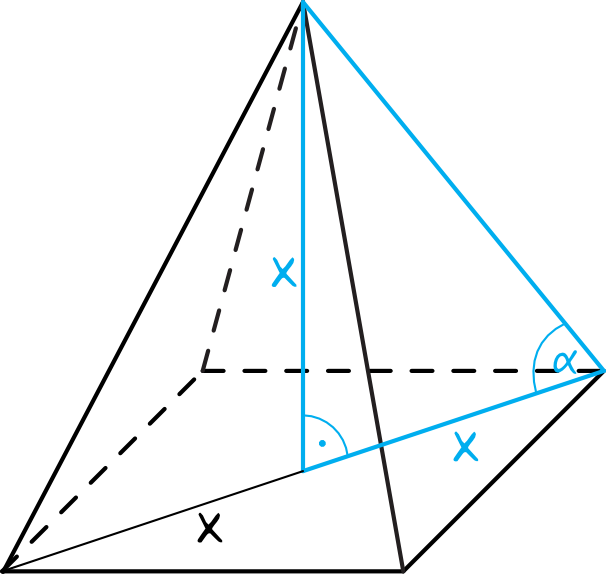
Widzimy wyraźnie, że połowa długości przekątnej podstawy, wysokość bryły oraz krawędź boczna tworzą trójkąt prostokątny z którego będziemy teraz obliczać interesujący nas kąt.
Krok 2. Obliczenie miary kąta nachylenia krawędzi bocznej do płaszczyzny podstawy.
Powinniśmy dostrzec, że przyprostokątne naszego trójkąta prostokątnego mają jednakową długość. To z kolei prowadzi nas do wniosku, że ten trójkąt jest równoramienny, czyli że jest to klasyczny trójkąt o kątach \(45°, 45°, 90°\), bo tylko taki trójkąt jest jednocześnie prostokątny i równoramienny. Stąd też bez żadnych dodatkowych obliczeń możemy być pewni, że kąt nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy \(45°\).