Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
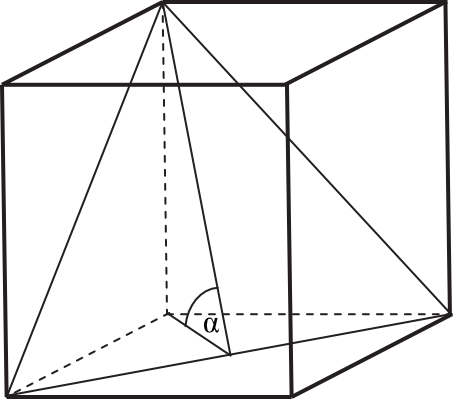
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt \(α\) o mierze:
Jeżeli wysokość graniastosłupa oznaczymy sobie literą \(h\), to z treści zadania wynika, że długość przekątnej podstawy graniastosłupa (podstawy! nie bryły jako takiej) jest równa \(2h\).
Dodatkowo wiemy, że w podstawie graniastosłupa jest kwadrat (a wiemy to stąd, że jest to graniastosłup prawidłowy czworokątny). To oznacza, że jego przekątne przecinają się dokładnie w połowie swojej długości, a co za tym idzie – odcinek \(BC\) ma długość \(h\) (patrz rysunek). Wygląda to mniej więcej tak:
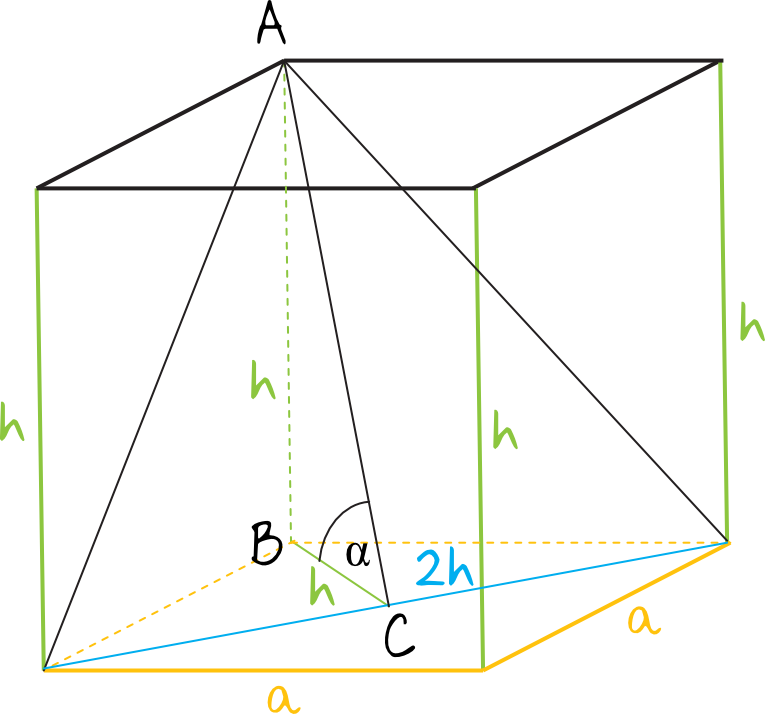
Z naszej analizy wynika, że powstał nam trójkąt \(ABC\), który jest prostokątny i równoramienny, a to z kolei oznacza że jest to trójkąt o kątach których miara wynosi \(45°, 45°, 90°\). Poszukiwany przez nas kąt \(α\) ma więc \(45°\).
B. \(45°\)

