Rozwiązanie
Krok 1. Dostrzeżenie podobieństwa prostokątów i zapisanie stosunku długości boków.
W zadaniu mamy do czynienia z prostokątami podobnymi. Z treści zadania wynika, że ten mały prostokąt \(AEFG\) ma wymiary \(40\times30\), zatem stosunek długości boków wynosi tutaj \(40:30\), czyli \(4:3\). Analogiczny stosunek długości boków musi więc wystąpić w tym drugim prostokącie, zatem możemy zapisać, że bok \(AB=4x\) oraz \(BC=3x\).
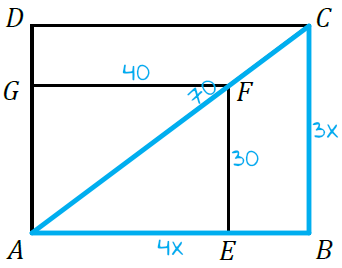
Krok 2. Obliczenie długości boków prostokąta \(ABCD\).
Spójrzmy na trójkąt \(ABC\). Jest to trójkąt prostokątny w którym przyprostokątne mają długość \(3x\) oraz \(4x\), a przeciwprostokątna jest równa \(70\) (zgodnie z treścią zadania). Skoro tak, to korzystając z Twierdzenia Pitagorasa, możemy zapisać, że:
$$(3x)^2+(4x)^2=70^2 \\
9x^2+16x^2=4900 \\
25x^2=4900 \\
x^2=196 \\
x=14 \quad\lor\quad x=-14$$
Ujemną długość oczywiście odrzucamy, zatem zostaje nam \(x=14\).
Skoro tak, to długości boków naszego prostokąta będą następujące:
$$|AB|=4x=4\cdot14=56 \\
|BC|=3x=3\cdot14=42$$
Wiemy już zatem, że nasz duży prostokąt ma wymiary \(56\times42\).
Krok 3. Obliczenie obwodu prostokąta \(ABCD\).
Na koniec została już tylko formalność, czyli obliczenie obwodu tej figury:
$$Obw=2\cdot56+2\cdot42 \\
Obw=112+84 \\
Obw=196$$