Przekątna \(AC\) prostokąta \(ABCD\) ma długość \(14\). Bok \(AB\) tego prostokąta ma długość \(6\). Długość boku \(BC\) jest równa:
\(8\)
\(4\sqrt{10}\)
\(2\sqrt{58}\)
\(10\)
Rozwiązanie:
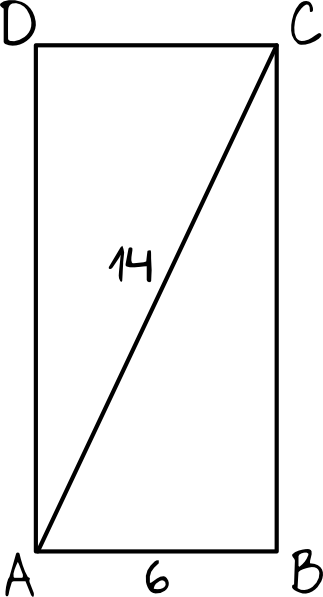
Z rysunku bardzo jasno wynika, że przy wyliczeniu długości boku \(BC\) musimy posłużyć się Twierdzeniem Pitagorasa.
$$|AB|^2+|BC|^2=|AC|^2 \\
6^2+|BC|^2=14^2 \\
36+|BC|^2=196 \\
|BC|^2=160 \\
|BC|=\sqrt{160} \\
|BC|=\sqrt{16\cdot10}=4\sqrt{10}$$
Odpowiedź:
B. \(4\sqrt{10}\)

