Przekątna \(AC\) prostokąta \(ABCD\) ma długość \(11\), a bok \(AB\) jest od niej o \(5\) krótszy. Oblicz długość boku \(AD\).
\(\sqrt{157}\)
\(\sqrt{85}\)
\(5\)
\(\sqrt{83}\)
Rozwiązanie:
Z treści zadania wynika, że \(|AB|=11-5=6\). To jednocześnie oznacza, że także \(|CD|=6\). Zróbmy sobie jeszcze dla pewności rysunek pomocniczy:
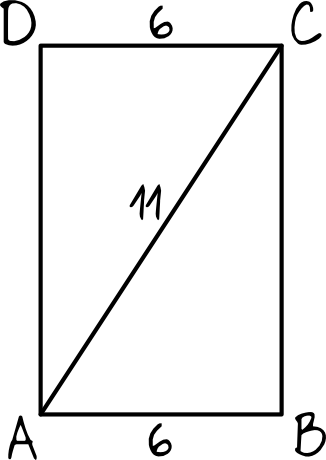
Musimy teraz obliczyć długość odcinka \(AD\), co oczywiście możemy zrobić za pomocą Twierdzenia Pitagorasa:
$$|AD|^2+|CD|^2=|AC|^2 \\
|AD|^2+6^2=11^2 \\
|AD|^2+36=121 \\
|AD|^2=85 \\
|AD|=\sqrt{85}$$
Odpowiedź:
B. \(\sqrt{85}\)

