Przedziały liczbowe

Przedziały liczbowe są matematyczną prezentacją pewnego zakresu liczb, który nas interesuje. Za pomocą przedziałów będziemy więc mogli zapisać informację o tym, że jakaś liczba jest np. większa od \(7\) albo też, że jest większa od \(3\) i jednocześnie mniejsza od \(10\).

Przedziały liczbowe zapisujemy zazwyczaj w jednej z trzech form:
a) za pomocą znaków nierówności
Tutaj będziemy posługiwać się czterema znakami: \(\lt, \gt, \le, \ge\)
Znaki \(\lt\) oraz \(\gt\) informują nas, że dana krańcowa liczba nie należy do przedziału. Znaki \(\le\) oraz \(\ge\) informują nas, że dana krańcowa liczba do tego przedziału należy.
Przykładowymi zapisami będą np. \(x\gt1,\;x\le6\), a także \(5\lt x\le9\).

b) za pomocą zapisu typu \(x\in\)
W tego typu zapisach będziemy posługiwać się nawiasami otwartymi \((\) i \()\) oraz domkniętymi \(\langle\) i \(\rangle\). Nawias otwarty oznacza, że dana krańcowa liczba nie należy do przedziału. Nawias domknięty informuje nas, że dana krańcowa liczba należy do przedziału.
Przykładowymi zapisami będą np. \(x\in(1;+\infty),\;x\in(-\infty;6\rangle\) oraz \(x\in(5;9\rangle\).

c) graficznej, czyli na osi liczbowej
Tutaj kluczowe będą kropki, które będziemy rysować przy danej liczbie. Kropka niezamalowana oznaczać będzie, że dana liczba do tego przedziału nie należy, a kropka zamalowana informuje nas, że dana krańcowa liczba mieści się w danym przedziale. Przykładowo:

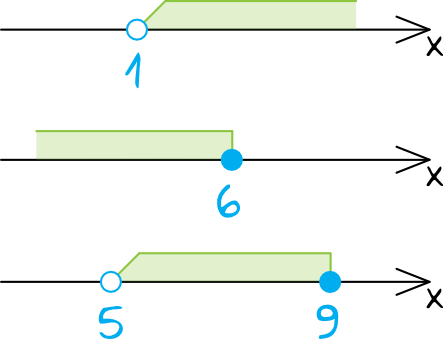
Spróbujmy sobie omówić nieco dokładniej kilka przedziałów, które są zapisane w każdej z tych omawianych form.

Przykład 1.
$$x\gt3 \\
x\in(3;+\infty)$$

Wszystkie te zapisy znaczą dokładnie to samo. Każdy z nich informuje nas, że wartość \(x\) jest większa od \(3\). To co ważne, to fakt, że liczba \(3\) do tych przedziałów nie należy. Do przedziałów należą tylko wartości większe od \(3\).

Przykładowymi liczbami mieszczącymi się w każdym tym przedziale będzie więc np. \(5, \sqrt{33}\) oraz \(3,01\).

Przykład 2.
$$x\ge3 \\
x\in\langle3;+\infty)$$

Te zapisy są bardzo podobne do tych z pierwszego przykładu, ale tym razem każdy z nich informuje nas, że nasz \(x\) jest większy lub równy \(3\). W przypadku postaci ze znakiem nierówności świadczy o tym fakt użycia znaku \(\ge\), w przypadku zapisu przedziału z użyciem znaku \(\in\) mamy ostry nawias po lewej stronie, a w formie graficznej przy wartości \(3\) pojawiła się zamalowana kropka. Możemy więc powiedzieć, że w przeciwieństwie do poprzedniego przykładu, tutaj liczba \(3\) mieści się w naszych przedziałach.

Przykładowymi liczbami mieszczącymi się w każdym tym przedziale będą zatem np. \(3\frac{1}{10}, 170\) oraz właśnie \(3\).

Przykład 3.
$$-2\lt x\le8 \\
x\in(-2;8\rangle$$

Te zapisy mówią nam, że \(x\) musi być większy od \(-2\) i jednocześnie musi być mniejszy lub równy \(8\). Można więc powiedzieć, że \(-2\) do tego przedziału nie należy, ale za to liczba \(8\) już się w tym przedziale mieści.

Przykładowymi liczbami mieszczącymi się w każdym tym przedziale będą zatem \(-\frac{1}{2}, 0, \sqrt{3}\) oraz właśnie \(8\).

Najważniejszą informacją płynącą z tych powyższych przykładów jest dostrzeżenie tego, że kiedy mamy znaki \(\le, \ge\) lub ostre nawiasy \(\langle, \rangle\) lub zamalowane kropki, to krańcowa liczba takiego zapisu należy do tego przedziału.