Rozwiązanie
Krok 1. Wyznaczenie wymiarów szarej części paska.
Szara część jest prostokątem. O tym prostokącie wiemy, że ma wysokość \(2cm\) i że ma pole \(8cm^2\), czyli długość tego prostokąta wynosi:
$$a\cdot2cm=8cm^2 \\
a=4cm$$
Krok 2. Obliczenie pola powierzchni białej części paska.
Biała część paska jest trapezem, w którym wysokość ma miarę \(h=2cm\), dłuższa podstawa ma miarę \(a=12cm-4cm=8cm\), natomiast krótsza podstawa ma \(b=8cm-2cm=6cm\).
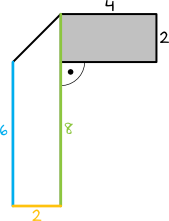
Pole tej figury będzie zatem równe:
$$P=\frac{1}{2}(a+b)\cdot h \\
P=\frac{1}{2}\cdot(8cm+6cm)\cdot2cm \\
P=\frac{1}{2}\cdot14cm\cdot2cm \\
P=14cm^2$$
Jeżeli nie dostrzegliśmy tego, że jest to trapez to mogliśmy też zauważyć że nasza biała część ma pole powierzchni równe powierzchni prostokąta o wymiarach \(8cm\times2cm\), pomniejszonego o trójkąt prostokątny o przyprostokątnych \(2cm\) i \(2cm\) (patrz rysunek):
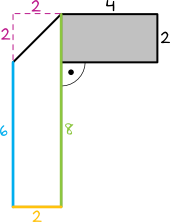
Wtedy:
$$P=P_{prostokąta}-P_{trójkąta} \\
P=8cm\cdot2cm-\frac{1}{2}\cdot2cm\cdot2cm \\
P=16cm^2-2cm^2 \\
P=14cm^2$$