Rozwiązanie
Aby dobrze opisać co będziemy liczyć, to oznaczmy sobie zacieniony kawałek kąta przy boku \(AE\) jako \(α\), natomiast zacieniony kawałek kąta przy boku \(AD\) jako \(β\).
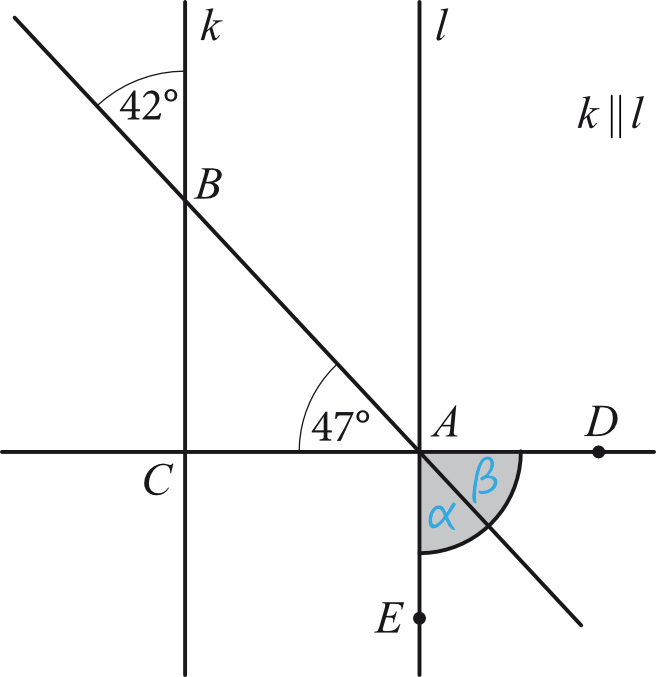
Krok 1. Obliczenie miary kąta \(α\).
Spróbujmy ustalić jaka jest miara zacienionego kąta \(α\). Powinniśmy dostrzec, że ten kąt oraz kąt o mierze \(42°\) są kątami naprzemianległymi, zatem będą one miały jednakową miarę. Z tego też względu \(α=42°\).
Krok 2. Obliczenie miary kąta \(β\).
Kąt o mierze \(47°\) oraz nasz kąt \(β\) tworzą parę kątów wierzchołkowych. Z własności kątów wierzchołkowych wynika, że mają one tą samą miarę, stąd też możemy zapisać, że \(β=47°\).
Krok 3. Obliczenie miary zacienionego kąta.
Nasz zacieniony kąt jest sumą miar kątów \(α\) oraz \(β\), zatem jego miara wyniesie:
$$42°+47°=89°$$
Zacieniony kąt jest więc kątem ostrym.