Proste a i b są równoległe. Półproste PA i PB przecinają te proste, w wyniku czego tworzą z nimi kąty ostre

I sposób - przeprowadzając prostą przez punkt \(P\):
Jeżeli przez punkt \(P\) poprowadzimy prostą równoległą do prostych \(a\) oraz \(b\), to korzystając z własności kątów odpowiadających otrzymamy następującą sytuację:


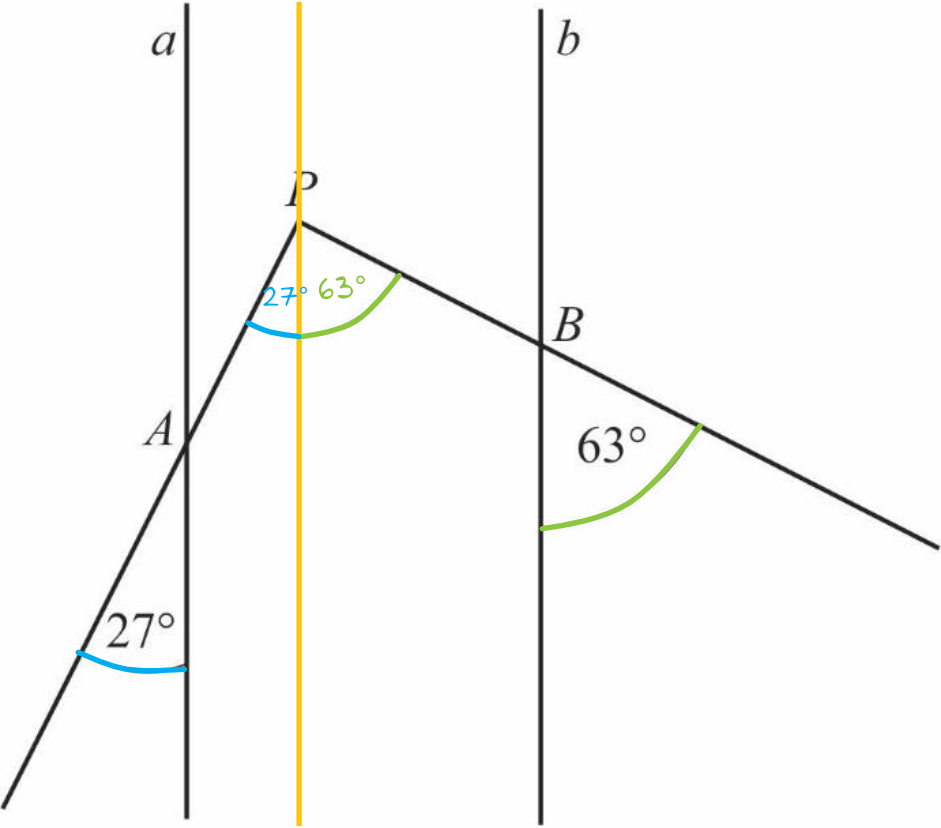
Suma kątów \(27°+63°\) daje kąt \(90°\) i właśnie to należało udowodnić.

II sposób - przedłużając półprostą \(PB\):
Jeżeli przedłużymy półprostą \(PB\) tak aby przecięła się z prostą \(a\) to otrzymamy trójkąt \(ACP\) którego dwa kąty wyznaczymy z własności kątów:
\(|\sphericalangle CAP|=27°\) (kąt wierzchołkowy)
\(|\sphericalangle ACP|=63°\) (kąt odpowiadający)


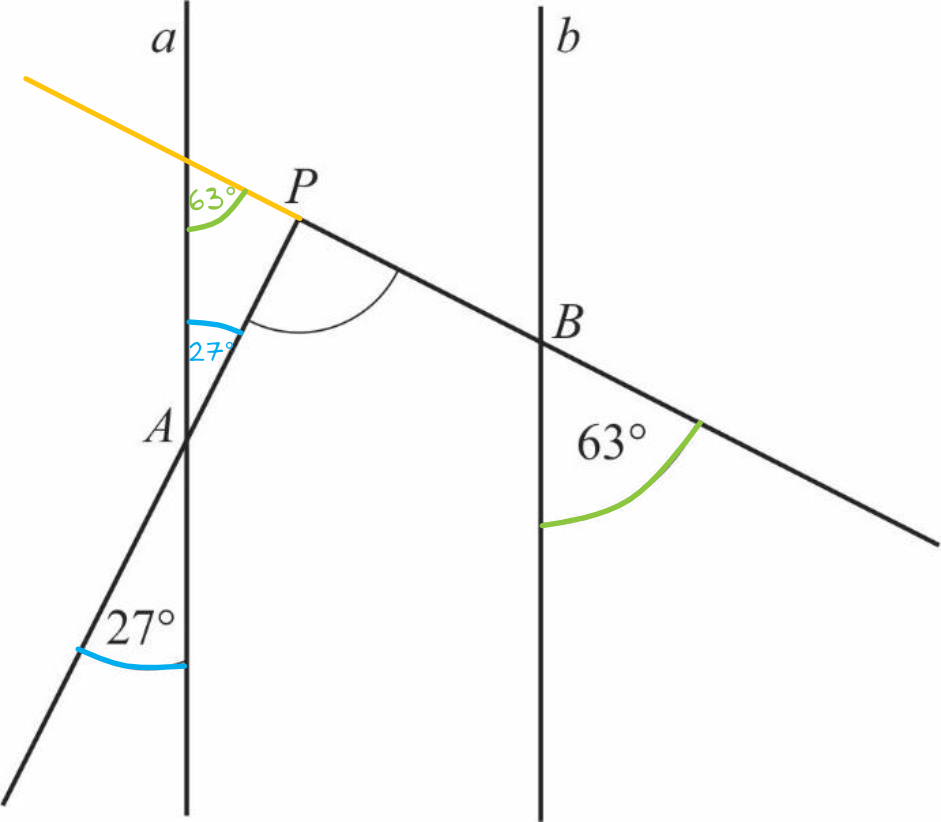
To oznacza, że kąt \(CPA\) ma miarę:
$$180°-27°-63°=90°$$

Kąty \(CPA\) oraz poszukiwany przez nas \(APB\) są kątami przyległymi (czyli takimi których łączna miara wynosi \(180°\)). Skoro \(|\sphericalangle CPA|=90°\), to:
$$|\sphericalangle APB|=180°-90°=90°$$