Prosta określona wzorem y=ax+1 jest symetralną odcinka AB, gdzie A=(-3,2) i B=(1,4)

Prosta określona wzorem $y=ax+1$ jest symetralną odcinka $AB$, gdzie $A=(-3,2)$ i $B=(1,4)$. Wynika stąd, że:

$a=-\frac{1}{2}$

$a=\frac{1}{2}$

$a=-2$

$a=2$

Rozwiązanie:

Zanim przejdziemy do obliczeń to omówmy sobie co tak naprawdę musimy obliczyć. Mamy podane współrzędne punktu $A$ i $B$, które tworzą odcinek w układzie współrzędnych. Przez ten odcinek poprowadzono prostą symetralną (czyli tak naprawdę prostopadłą do tego odcinka, która przechodzi przez jego środek). Naszym zadaniem jest obliczenie współczynnika kierunkowego $a$ tej prostej symetralnej.

Krok 1. Obliczenie współczynnika kierunkowego prostej $AB$.

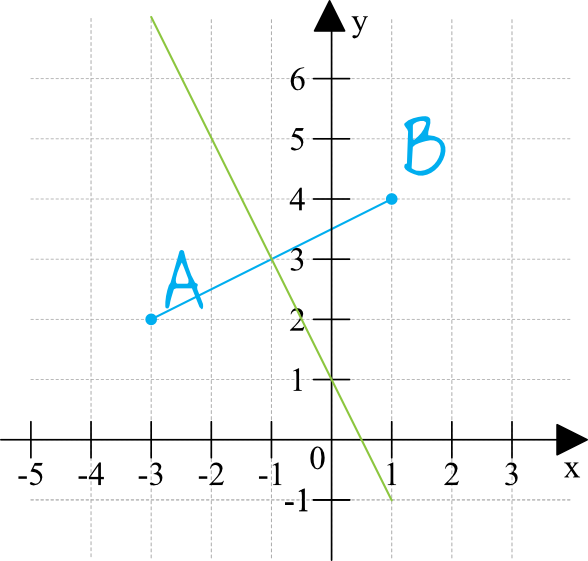
Zanim obliczymy współczynnik kierunkowy symetralnej, to potrzebny nam będzie współczynnik kierunkowy prostej na której znajduje się odcinek $AB$. Obliczymy go za pomocą wzoru:
$$m=\frac{y_{B}-y_{A}}{x_{B}-x_{A}} \\
m=\frac{4-2}{1-(-3)} \\
m=\frac{2}{4} \\
m=\frac{1}{2}$$

Krok 2. Obliczenie współczynnika kierunkowego prostej $y=ax+1$.

Tak jak wcześniej ustaliliśmy – skoro jest to symetralna odcinka $AB$, to znaczy że jest to prosta prostopadła. Aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy $-1$, zatem:
$$a\cdot m=-1 \\
a\cdot\frac{1}{2}=-1 \\
a=-2$$

Odpowiedź:

C. $a=-2$

Zadania

Prosta określona wzorem y=ax+1 jest symetralną odcinka AB, gdzie A=(-3,2) i B=(1,4)

Prosta określona wzorem \(y=ax+1\) jest symetralną odcinka \(AB\), gdzie \(A=(-3,2)\) i \(B=(1,4)\). Wynika stąd, że: