Rozwiązanie
Krok 1. Wyznaczenie współrzędnej \(p\) wierzchołka paraboli.
Z własności parabol wiemy, że oś symetrii przechodzi dokładnie przez wierzchołek paraboli.
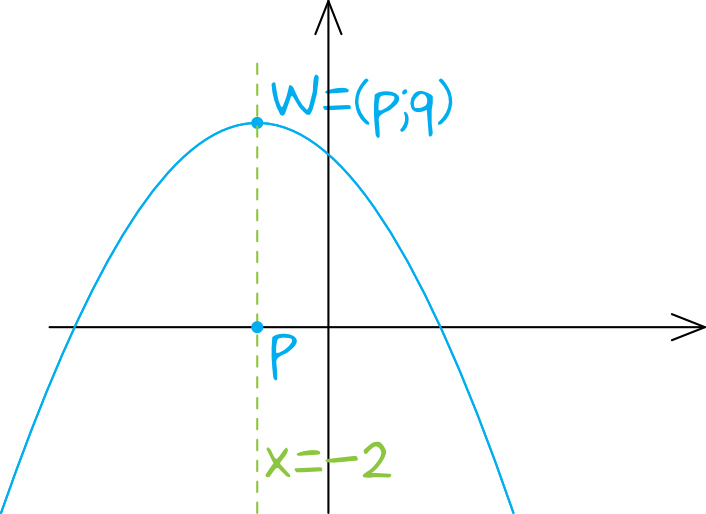
To z kolei oznacza, że skoro prosta o równaniu \(x=-2\) jest osią symetrii, to współrzędna \(p\) wierzchołka naszej paraboli będzie równa \(p=-2\).
Krok 2. Obliczenie wartości współczynnika \(a\).
Skorzystamy ze wzoru na współrzędną \(p\) wierzchołka paraboli, czyli ze wzoru \(p=\frac{-b}{2a}\). Ze wzoru funkcji \(f(x)=ax^2-8x+c\) możemy odczytać, że \(b=8\), zatem:
$$p=\frac{-b}{2a} \\
-2=\frac{-(-8)}{2a} \\
-2=\frac{8}{2a} \\
-4a=8 \\
a=-2$$
To oznacza, że nasza funkcja przyjmie postać \(f(x)=-2x^2-8x+c\). Do pełnego wzoru brakuje nam jeszcze wartości współczynnika \(c\).
Krok 3. Obliczenie wartości współczynnika \(c\).
Do poznania wartości współczynnika \(c\) posłuży nam informacja o tym, że punkt \(P=(2,2)\) należy do wykresu tej funkcji. Podstawiając współrzędne tego punktu do wyznaczonej już w poprzednim kroku postaci wzoru ze współczynnikiem \(a\) otrzymamy:
$$f(x)=-2x^2-8x+c \\
2=-2\cdot2^2-8\cdot2+c \\
2=-2\cdot4-8\cdot2+c \\
2=-8-16+c \\
2=-24+c \\
c=26$$
W treści zadania prosili nas o wyznaczenie współczynnika \(a\) oraz \(c\), zatem możemy zapisać, że \(a=-2\) oraz \(c=26\).