Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować sobie tę sytuację na rysunku pomocniczym:
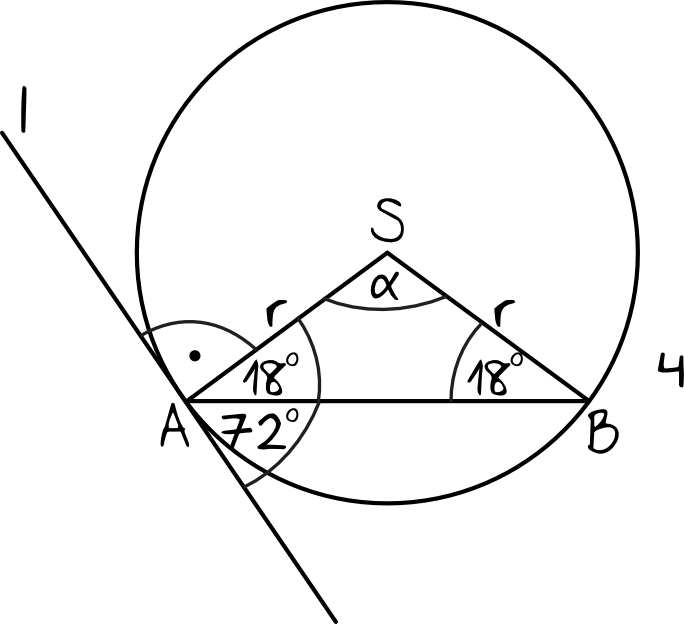
Trójkąt \(ABS\) jest na pewno równoramienny (bo dwa ramiona mają długość równą promieniowi okręgu). Dodatkowo wiemy, że styczna do okręgu tworzy z promieniem okręgu przechodzącym przez punkt styczności kąt \(90°\). Stąd też jesteśmy w stanie obliczyć, że kąty \(BAS\) oraz \(ABS\) mają miarę: \(90°-72°=18°\).
Krok 2. Obliczenie miary kąta \(ASB\).
W trójkącie suma miar kątów jest równa \(180°\). To oznacza, że kąt \(ASB\) ma miarę:
$$|\sphericalangle ASB|=180°-18°-18°=144°$$