Wzór na pole trapezu jest chyba jednym z najbardziej złożonych wzorów na pola figur jakie poznajemy na matematyce, dlatego też odpowiemy sobie na pytanie skąd ten wzór się wziął i jak wygląda w ostatecznej wersji.
Gdybyśmy wycięli z papieru dwa identyczne trapezy, to moglibyśmy po ich odpowiednim obróceniu ułożyć równoległobok. To znaczy, że pole takiego jednego małego trapezu jest równe połowie tego dużego równoległoboku, który nam powstanie. Spójrz na poniższy rysunek, który wyjaśni Ci wszelkie wątpliwości:
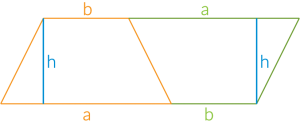
Pole jednego trapezu (pomarańczowego lub zielonego) jest równe połowie równoległoboku, który nam powstał.
To właśnie z tej zależności powstał nam wzór na pole trapezu. W podstawie równoległoboku mamy bok o długości \(a+b\), a do tego znaną nam wysokość \(h\). Przed chwilą sobie też powiedzieliśmy, że taki jeden trapez ma powierzchnię równą połowie tego dużego równoległoboku. Te wszystkie zależności opisano następującym wzorem:
$$P=\frac{1}{2}\cdot(a+b)\cdot h$$
gdzie:
\(P\) – pole trapezu
\(a\), \(b\) – długości podstaw trapezu
\(h\) – wysokość trapezu
Więcej informacji na temat trapezów znajdziesz tutaj:

Super stronka polecam. By człowiek Krzak