Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania wyglądać będzie następująco:
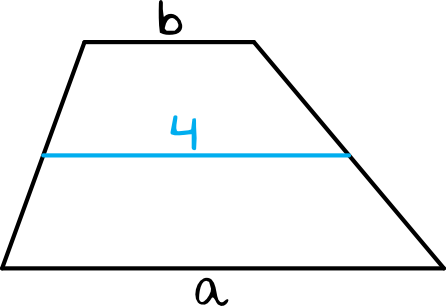
Wskazany odcinek o długości \(4cm\) łączy środki ramion trapezu. Z własności trapezów wynika, że długość łącząca środki trapezu jest równa połowie długości sumy dolnej i górnej podstawy, czyli że:
$$\frac{a+b}{2}=4 \\
a+b=8$$
Jeżeli jednak nie pamiętamy o tej własności (a nie ukrywajmy, jest ona bardzo specyficzna i rzadko wykorzystywana), to wystarczy dorysować sobie obok drugi (odwrócony) trapez i wtedy dostrzeżemy, że \(a+b=2\cdot4=8\).

Krok 2. Obliczenie wysokości trapezu.
Korzystając ze wzoru na pole trapezu i wiedząc, że \(P=20cm^2\) oraz że \(a+b=8\) możemy obliczyć wysokość trapezu:
$$P=\frac{1}{2}(a+b)\cdot h \\
20=\frac{1}{2}\cdot8\cdot h \\
20=4\cdot h \\
h=5[cm]$$