Aby obliczyć pole równoległoboku musimy znać:
- długość jednego z jego boków
- wysokość opuszczoną na ten bok
$$P=a\cdot h$$
gdzie:
\(P\) – pole równoległoboku
\(a\) – długość boku
\(h\) – wysokość opuszczona na ten bok
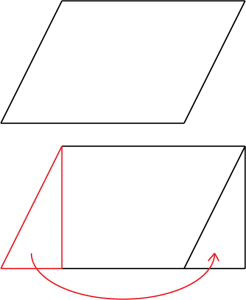
Jak widzisz, ten wzór jest bardzo podobny do wzoru prostokąta (\(P=a\cdot b\)) i ta zbieżność nie jest przypadkowa. Spójrz na poniższy rysunek:
Jeśli odetniemy kawałek równoległoboku wzdłuż jego wysokości, to otrzymamy trójkąt, który idealnie wpasuje się nam w przestrzeń po drugiej stronie figury, tworząc w ten sposób… prostokąt. To dlatego te wzory są niemal identyczne. Ty tę własność możesz wykorzystać w sytuacji, w której zapomnisz jaki był dokładny wzór na pole równoległoboku.
Identyczny wzór możemy zastosować także do rombu, ale w przypadku tej figury mamy jeszcze jeden specjalny wzór, w którym wykorzystamy długości przekątnych.
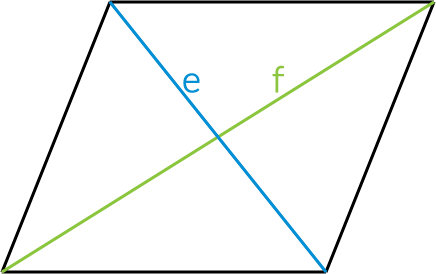
$$P=\frac{1}{2}e\cdot f$$
gdzie:
\(P\) – pole rombu
\(e\), \(f\) – długości przekątnych rombu
Pole równoległoboku i rombu jest równe iloczynowi długości boku i wysokości opuszczonej na ten bok.
Pole rombu jest równe połowie iloczynu długości przekątnych.
W matematyce na poziomie technikum lub liceum posługujemy się także nieco bardziej rozbudowanymi formami wzorów na pole równoległoboku i rombu. Oto one:
Dodatkowe wzory na pole równoległoboku:
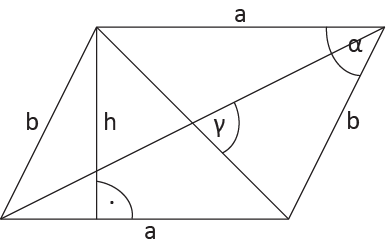
$$P=a\cdot b \cdot sin\alpha\\
P=\frac{1}{2}d_{1}\cdot d_{2}\cdot sin\gamma$$
Dodatkowe wzory na pole rombu:
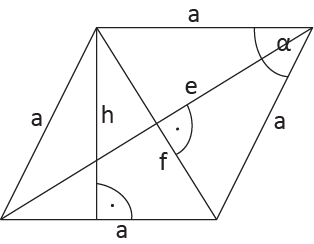
$$P=a^2 \cdot sin\alpha\\
P=\frac{1}{2}d_{1}\cdot d_{2}$$
Z jakimi zadaniami możemy się spotkać w tym temacie?
Podobnie jak to miało miejsce w przypadku np. trójkąta, tak i tutaj za pomocą wzorów na powierzchnię będziemy mogli obliczać nie tylko powierzchnię samą w sobie, ale także różne długości i wysokości poszczególnych figur (odpowiednio przekształcając poszczególne wzory). Jeśli chcesz przećwiczyć obliczanie prostych przykładów z polem rombu i równoległoboku to zapraszam Cię do tych tematów:

hmmm przydatne dziękuje
fajne wytłumaczenie dziękuje
bardzo fajne można przypomnieć przed lekcją
uczyłam sie z tego do sprawdzianu i napisałam na 6