Pole powierzchni całkowitej prostopadłościanu jest równe \(198\). Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to \(1:2:3\). Oblicz długość przekątnej tego prostopadłościanu.
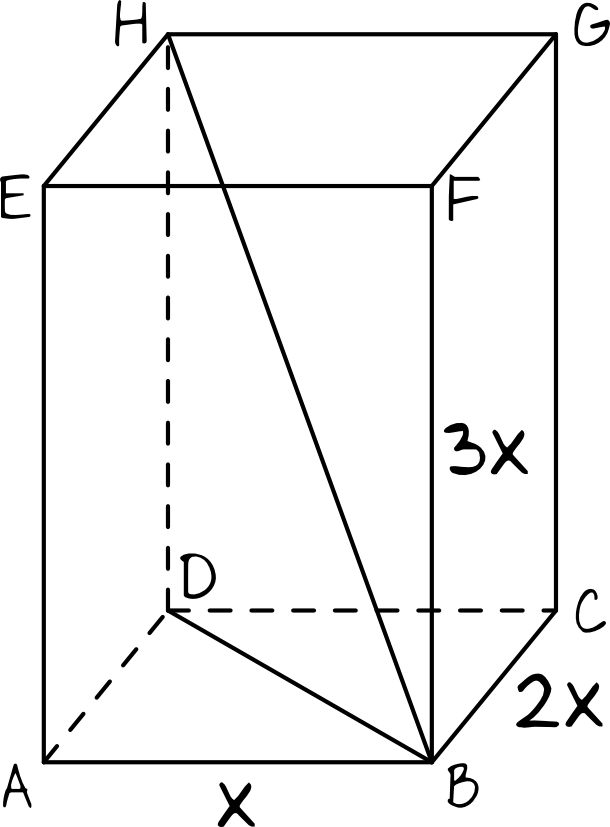
Znając pole powierzchni całkowitej prostopadłościanu i relacje między poszczególnymi długościami boków (patrz rysunek z pierwszego kroku) możemy obliczyć długość każdej z krawędzi.
$$P_{c}=2\cdot x\cdot2x+2\cdot x\cdot3x+2\cdot2x\cdot3x \\
198=4x^2+6x^2+12x^2 \\
198=22x^2 \\
x^2=9 \\
x=3 \quad\lor\quad x=-3$$
Ujemną długość oczywiście odrzucamy, zostaje nam \(x=3\).
Znając wartość \(x=3\) znamy tak naprawdę długości wszystkich krawędzi tego prostopadłościanu: \(x=3\), \(2x=6\) oraz \(3x=9\).
Musimy poznać długość odcinka \(BD\), tak aby potem użyć jej do obliczenia przekątnej bryły. Z Twierdzenia Pitagorasa wynika, że:
$$a^2+b^2=c^2 \\
|AB|^2+|AD|^2=|BD|^2 \\
3^2+6^2=|BD|^2 \\
9+36=|BD|^2 \\
|BD|^2=45 \\
|BD|=\sqrt{45}$$
Ponownie skorzystamy ze wzoru na Twierdzenie Pitagorasa.
$$|BD|^2+|DH|^2=|BH|^2 \\
(\sqrt{45})^2+9^2=|BH|^2 \\
45+81=|BH|^2 \\
|BH|^2=126 \\
|BH|=\sqrt{126}=\sqrt{9\cdot14}=3\sqrt{14}$$
Przekątna prostopadłościanu ma długość \(3\sqrt{14}\).


nie ma może innych, krótszych rozwiązań?
Nie rozwiązuję zadań byle jak, bo to ma też być materiał do nauki, tak aby każdy wiedział co z czego się bierze ;) Jednak jeśli nie potrzebujesz tak rozpisanego zadania, to wystarczy że spojrzysz na same liczby/wyniki, raczej prościej się tego zrobić nie da ;)
Dlaczego w twierdzeniu Pitagorasa (krok trzeci) jest IABI^2 +IADI^2= IBDI^2
Myślałam, że to IABI jest przeciwprostokątną i że powinno być IBDI^2+ IADI^2= IABI^2.
Gdzie robię błąd i dlaczego powinno być tak jak w rozwiązaniu zamieszczonym na tej stronie? Z góry dziękuję za odpowiedź ;-)
Spoglądamy na trójkąt ABD :) Bok AB nie jest przeciwprostokątną, tylko przyprostokątną :)
Cześć, dlaczego tworzymy rysunek poglądowy akurat w taki sposób? Tzn. dlaczego |AB| = x, |BC| = 2x, |BF| = 3x? Czy zawsze tak mamy podchodzić do tego typu zadań, gdy jest podany stosunek tak jak tu 1:2:3, że te kolejne liczby wyznaczają kierunek?
Jeśli nie, to wydaje się, że formalnie powinniśmy rozważyć też inne przypadki, np. |AB| = x, |BC| = 3x i |BF| = 2x.
Możesz oznaczyć dowolnie – to co proponujesz będzie dokładnie takim samym prostopadłościanem, tylko położonym na boku ;) W obliczeniach (poza oznaczeniami) nic się więc nie zmieni.
dlaczego gdy podstawię wyliczone odpowiednio długości krawędzi tego prostopadłościanu do wzoru na przekątną prostopadłościanu, to wynik wychodzi inny niż przy liczeniu za pomocą pitagorasa ?
Prawdopodobnie popełniasz jakiś błąd rachunkowy ;)