Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest \(3\) razy dłuższa od krawędzi podstawy, jest równe \(140\). Zatem krawędź podstawy tego graniastosłupa jest równa:
\(\sqrt{10}\)
\(3\sqrt{10}\)
\(\sqrt{42}\)
\(3\sqrt{42}\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
Oznaczmy sobie jako \(a\) krawędź podstawy oraz \(3a\) jako wysokość graniastosłupa. Pamiętaj, że w podstawie graniastosłupa znajdzie się kwadrat, bo jest to graniastosłup prawidłowy czworokątny.
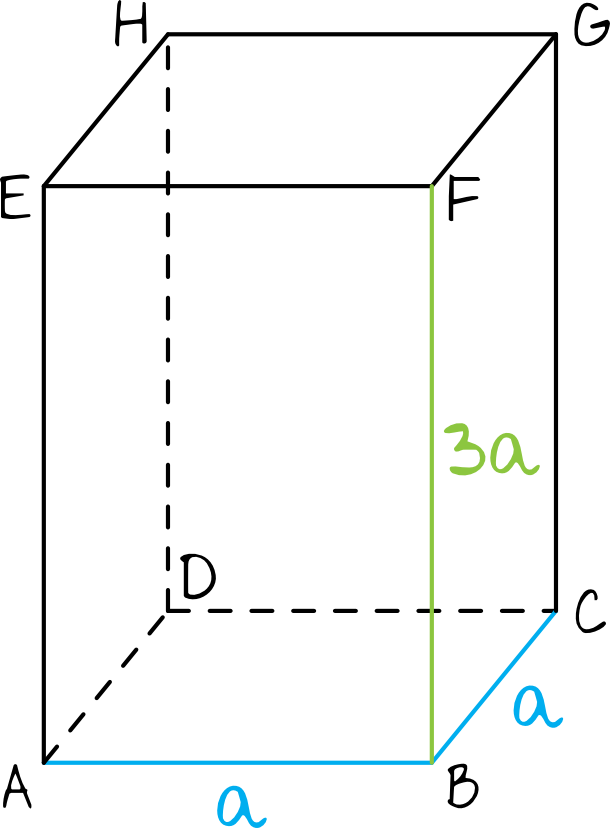
Krok 2. Zapisanie wzoru na pole podstawy i pole ściany bocznej.
Korzystając z rysunku i zawartych na nim oznaczeń zapiszmy sobie od razu wzory na pole powierzchni podstawy oraz na pole ściany bocznej:
$$P_{p}=a^2 \\
P_{b}=a\cdot3a=3a^2$$
Krok 3. Wyznaczenie długości krawędzi podstawy.
Skoro mamy dwie podstawy oraz cztery ściany boczne i znamy pole powierzchni całkowitej, to możemy ułożyć następujące równanie:
$$2P_{p}+4P_{b}=140 \\
2\cdot a^2+4\cdot3a^2=140 \\
2a^2+12a^2=140 \\
14a^2=140 \\
a^2=10 \\
a=\sqrt{10}$$
Odpowiedź:
A. \(\sqrt{10}\)


Super, bardzo pomogło