Pole powierzchni bocznej stożka o wysokości \(4\) i promieniu podstawy \(3\) jest równe:
\(9π\)
\(12π\)
\(15π\)
\(16π\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku pomocniczego.
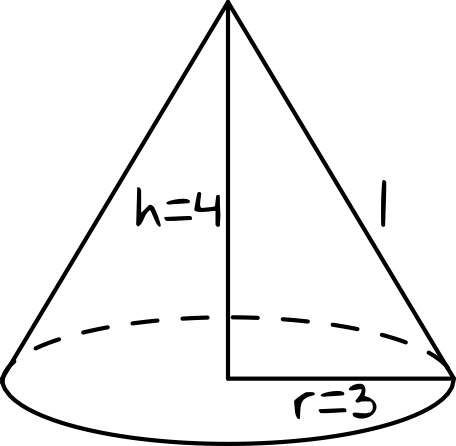
Znamy miarę \(h=4\) oraz \(r=3\). Nam jest potrzebna znajomość długość tzw. „tworzącej stożka” czyli \(l\), bo to dzięki niej wyliczymy pole powierzchni bocznej bryły. Skorzystamy tutaj oczywiście z Twierdzenia Pitagorasa.
Krok 2. Obliczenie długości tworzącej \(l\).
$$r^2+h^2=l^2 \\
l^2=3^2+4^2 \\
l^2=9+16 \\
l^2=25 \\
l=5 \quad\lor\quad l=-5$$
Ujemną wartość oczywiście odrzucamy, bo długość nie może być ujemna.
Krok 3. Obliczenie pola powierzchni bocznej stożka.
$$P_{b}=πrl=π\cdot3\cdot5=15π$$
Odpowiedź:
C. \(15π\)

