Rozwiązanie
Krok 1. Zapisanie zależności między polem powierzchni bocznej i polem podstawy.
Ze wzorów na pole powierzchni bocznej i pole podstawy wiemy, że:
$$P_{b}=\pi rl \\
P_{p}=\pi r^2$$
Z treści zadania wynika, że pole powierzchni bocznej jest trzy razy większe od pola podstawy, zatem:
$$P_{b}=3\cdot P_{p} \\
\pi rl=3\cdot(\pi r^2) \\
\pi rl=3\pi r^2 \\
rl=3r^2 \\
l=3r$$
Otrzymaliśmy informację, że \(l=3r\), czyli że tworząca stożka jest trzy razy dłuższa od promienia podstawy.
Krok 2. Sporządzenie rysunku pomocniczego.
Skoro \(l=3r\), to nasz stożek będzie wyglądał następująco:
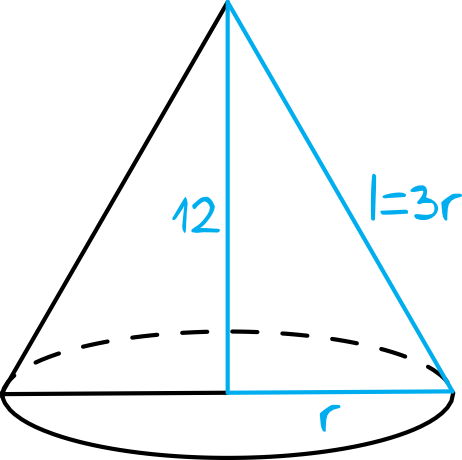
Utworzył nam się trójkąt prostokątny, w którym jedyną niewiadomą jest \(r\) i to właśnie z tego trójkąta obliczymy teraz długość promienia stożka.
Krok 3. Obliczenie długości promienia stożka.
Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$r^2+12^2=(3r)^2 \\
r^2+144=9r^2 \\
8r^2=144 \\
r^2=18 \\
r=\sqrt{18} \quad\lor\quad r=-\sqrt{18}$$
Ujemną wartość oczywiście odrzucamy, zatem zostaje nam \(r=\sqrt{18}\). Moglibyśmy jeszcze wyłączyć czynnik przed znak pierwiastka otrzymując \(r=3\sqrt{2}\), ale tutaj nie jest to potrzebne, bo i tak zaraz będziemy długość tego promienia podnosić do kwadratu.
Krok 4. Obliczenie objętości stożka.
Skoro \(H=12\) oraz \(r=\sqrt{18}\), to objętość stożka będzie równa:
$$V=\frac{1}{3}\cdot P_{p}\cdot H \\
V=\frac{1}{3}\cdot \pi r^2\cdot H \\
V=\frac{1}{3}\cdot \pi \cdot (\sqrt{18})^2\cdot12 \\
V=\frac{1}{3}\cdot \pi \cdot 18\cdot12 \\
V=72\pi$$