Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
W podstawie graniastosłupa prawidłowego czworokątnego jest kwadrat, a skoro jego pole jest równe \(36\), to każdy z boków ma długość \(a=6\). Nasz rysunek będzie więc wyglądał w ten oto sposób:
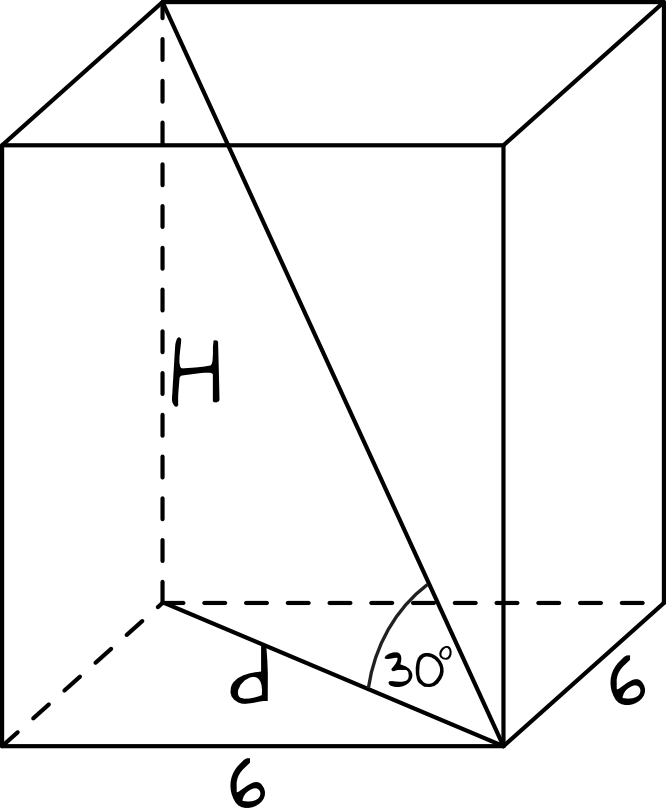
Krok 2. Obliczenie długości przekątnej podstawy.
Do obliczenia wysokości graniastosłupa będziemy za chwilę potrzebować długości przekątnej podstawy. Skoro w podstawie znajduje się kwadrat, to z własności przekątnych kwadratu wiemy, że kwadrat o boku \(a\) ma przekątną równą \(a\sqrt{2}\). W naszym przypadku \(a=6\), zatem przekątna ma długość \(d=6\sqrt{2}\).
Krok 3. Obliczenie wysokości graniastosłupa.
Korzystając z funkcji trygonometrycznych (a konkretnie z tangensa) możemy zapisać, że:
$$tgα=\frac{H}{d} \\
tg30°=\frac{H}{6\sqrt{2}} \\
\frac{\sqrt{3}}{3}=\frac{H}{6\sqrt{2}} \quad\bigg/\cdot6\sqrt{2} \\
H=\frac{\sqrt{3}\cdot6\sqrt{2}}{3} \\
H=\frac{6\sqrt{6}}{3} \\
H=2\sqrt{6}$$