Pole ćwiartki koła przedstawionej na rysunku jest równe 4 pi cm^2. Pole trójkąta ABC jest równe

Krok 1. Obliczenie pola powierzchni całego koła.
Skoro ćwiartka koła ma pole równe \(4πcm^2\), to całe koło ma pole powierzchni równe:
$$P=4\cdot4π cm^2 \\
P=16π cm^2$$

Krok 2. Obliczenie długości boków \(AB\) oraz \(BC\).
Boki \(AB\) oraz \(BC\) to tak naprawdę długość promienia koła, którego pole przed chwilą policzyliśmy:


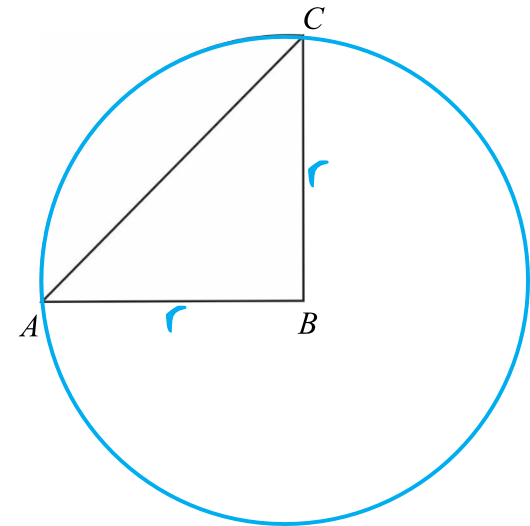
W związku z tym obliczając długość promienia koła poznamy długości kluczowych boków tego trójkąta. Długość promienia obliczymy korzystając ze wzoru na pole koła:
$$P=πr^2 \\
16πcm^2=πr^2 \\
r^2=16cm^2 \\
r=4cm$$

Krok 3. Obliczenie pola trójkąta \(ABC\).
Skoro boki \(AB\) oraz \(BC\) mają długość \(4cm\), to pole tego trójkąta będzie równe:
$$P=\frac{1}{2}\cdot4cm\cdot4cm \\
P=8cm^2$$